Để đảm bảo sức khỏe cho các thành viên, Một Gia đình Cần ít Nhất 900 đơn Vị Protein mỗi ngày từ các nguồn thực phẩm khác nhau. Việc tính toán lượng protein cần thiết và lựa chọn thực phẩm phù hợp là vô cùng quan trọng. Bài viết này sẽ cung cấp một phương pháp tiếp cận để giải quyết bài toán dinh dưỡng này, tập trung vào hai nguồn protein phổ biến là thịt bò và thịt lợn.
Giả sử gia đình mua x kg thịt bò và y kg thịt lợn. Theo yêu cầu về số lượng, ta có các ràng buộc sau:
- 0 ≤ x ≤ 1,6 (Số kilôgam thịt bò mua không quá 1,6kg)
- 0 ≤ y ≤ 1,1 (Số kilôgam thịt lợn mua không quá 1,1kg)
Mỗi kilôgam thịt bò chứa 800 đơn vị protein và mỗi kilôgam thịt lợn chứa 600 đơn vị protein. Do đó, lượng protein từ x kg thịt bò và y kg thịt lợn là: 800x + 600y (đơn vị). Vì gia đình cần ít nhất 900 đơn vị protein, ta có bất phương trình:
800x + 600y ≥ 900
Tương tự, mỗi kilôgam thịt bò chứa 200 đơn vị lipid và mỗi kilôgam thịt lợn chứa 400 đơn vị lipid. Lượng lipid từ x kg thịt bò và y kg thịt lợn là: 200x + 400y (đơn vị). Gia đình cần ít nhất 400 đơn vị lipid, nên ta có bất phương trình:
200x + 400y ≥ 400
Kết hợp các điều kiện trên, ta có hệ bất phương trình:
[left{ begin{array}{l}0 le x le 1,6\0 le y le 1,1\800x + 600y ge 900\200x + 400y ge 400end{array} right. Leftrightarrow left{ begin{array}{l}0 le x le 1,6\0 le y le 1,1\8x + 6y ge 9\x + 2y ge 2end{array} right.]
Bài toán này có thể được giải bằng phương pháp đồ thị, tìm ra miền nghiệm của hệ bất phương trình và xác định các điểm cực trị.
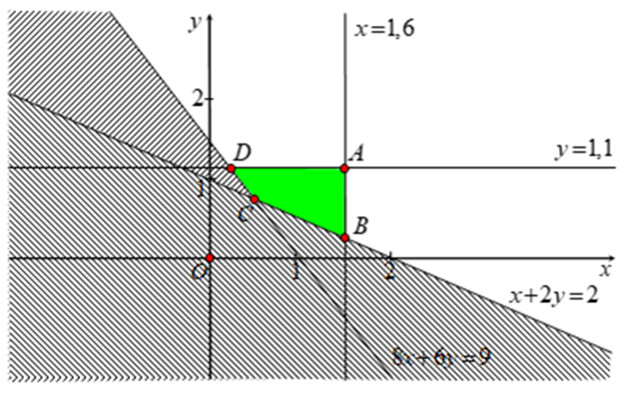 Đồ thị biểu diễn miền nghiệm của hệ bất phương trình về lượng protein và lipid cần thiết cho gia đình, với trục x là số kg thịt bò và trục y là số kg thịt lợn
Đồ thị biểu diễn miền nghiệm của hệ bất phương trình về lượng protein và lipid cần thiết cho gia đình, với trục x là số kg thịt bò và trục y là số kg thịt lợn
Giả sử miền nghiệm của hệ bất phương trình là tứ giác ABCD. Các đỉnh của tứ giác này biểu thị các phương án mua thịt bò và thịt lợn khác nhau, đảm bảo gia đình nhận đủ lượng protein và lipid cần thiết.
Để tối ưu chi phí, giả sử giá một kilôgam thịt bò là 250 nghìn đồng và giá một kilôgam thịt lợn là 160 nghìn đồng. Tổng chi phí mua x kg thịt bò và y kg thịt lợn là: F(x; y) = 250x + 160y (nghìn đồng).
Mục tiêu là tìm giá trị nhỏ nhất của F(x; y) trong miền nghiệm ABCD. Điều này có thể được thực hiện bằng cách tính giá trị của F(x; y) tại mỗi đỉnh của tứ giác và chọn ra giá trị nhỏ nhất.
Ví dụ, nếu các đỉnh của tứ giác ABCD là A(0,3; 1,1), B(0,6; 0,7), C(1,6; 0,2), D(1,6; 1,1), ta có:
- F(0,3; 1,1) = 250 . 0,3 + 160 . 1,1 = 251
- F(0,6; 0,7) = 250 . 0,6 + 160 . 0,7 = 262
- F(1,6; 0,2) = 250 . 1,6 + 160 . 0,2 = 432
- F(1,6; 1,1) = 250 . 1,6 + 160 . 1,1 = 576
Trong trường hợp này, chi phí thấp nhất là 251 nghìn đồng, đạt được khi mua 0,3 kg thịt bò và 1,1 kg thịt lợn.
Vậy, để đảm bảo một gia đình cần ít nhất 900 đơn vị protein mỗi ngày với chi phí tối ưu, cần mua 0,3 kilôgam thịt bò và 1,1 kilôgam thịt lợn. Bài toán này minh họa cách ứng dụng toán học vào việc lập kế hoạch dinh dưỡng hợp lý cho gia đình, giúp đảm bảo sức khỏe và tiết kiệm chi phí.