Trong hình học, một câu hỏi thú vị thường được đặt ra là: “Liệu mọi hình thoi đều có thể nội tiếp được trong một đường tròn hay không?”. Để trả lời câu hỏi này, chúng ta cần xem xét kỹ các đặc điểm của hình thoi và điều kiện để một tứ giác nội tiếp được đường tròn.
Trước hết, hãy cùng nhắc lại định nghĩa và tính chất của hình thoi.
Định nghĩa hình thoi: Hình thoi là một tứ giác có bốn cạnh bằng nhau.
Tính chất của hình thoi:
- Các cạnh đối song song.
- Các góc đối bằng nhau.
- Hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường.
- Hai đường chéo là các đường phân giác của các góc trong hình thoi.
Tiếp theo, chúng ta cần nắm vững điều kiện để một tứ giác nội tiếp được đường tròn.
Điều kiện để một tứ giác nội tiếp được đường tròn: Một tứ giác nội tiếp được đường tròn khi và chỉ khi tổng hai góc đối của tứ giác đó bằng 180 độ.
Bây giờ, chúng ta hãy xem xét liệu hình thoi có thỏa mãn điều kiện này hay không. Gọi ABCD là một hình thoi bất kỳ.
Để ABCD nội tiếp được trong một đường tròn, điều kiện cần và đủ là:
- ∠A + ∠C = 180°
- ∠B + ∠D = 180°
Vì hình thoi có các góc đối bằng nhau (∠A = ∠C và ∠B = ∠D), nên điều kiện trên trở thành:
- 2∠A = 180°
- 2∠B = 180°
Điều này suy ra:
- ∠A = 90°
- ∠B = 90°
Vậy, hình thoi ABCD chỉ nội tiếp được đường tròn khi tất cả các góc của nó đều bằng 90 độ. Điều này có nghĩa là hình thoi đó phải là hình vuông.
Kết luận: Không phải Mọi Hình Thoi đều Nội Tiếp được đường Tròn. Chỉ có hình vuông (một trường hợp đặc biệt của hình thoi) mới có thể nội tiếp được đường tròn.
Để hiểu rõ hơn về các hình có thể nội tiếp đường tròn, chúng ta sẽ xem xét một số ví dụ khác:
Hình chữ nhật:
Hình chữ nhật ABCD có các góc đều bằng 90 độ. Do đó, tổng hai góc đối bất kỳ của hình chữ nhật đều bằng 180 độ (90° + 90° = 180°). Vì vậy, hình chữ nhật luôn nội tiếp được trong một đường tròn. Tâm của đường tròn này là giao điểm của hai đường chéo, và bán kính của đường tròn bằng một nửa độ dài đường chéo.
Hình vuông nội tiếp đường tròn: Minh họa hình chữ nhật ABCD nội tiếp đường tròn, đường tròn có đường kính AC, thể hiện rõ các góc vuông.
Hình thang cân:
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. Trong hình thang cân ABCD (AB // CD và ∠A = ∠B), ta có ∠A + ∠D = 180° và ∠B + ∠C = 180°. Do đó, hình thang cân luôn nội tiếp được trong một đường tròn.
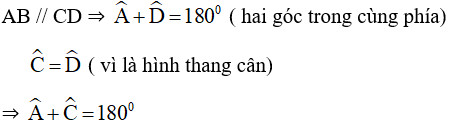Hình thang cân ABCD nội tiếp đường tròn thể hiện các góc bằng nhau và tính chất song song
Hình thang cân nội tiếp đường tròn: Mô tả hình thang cân ABCD nội tiếp đường tròn, nhấn mạnh tính chất các góc kề một đáy bằng nhau và hai đáy song song.
Tóm lại, để một tứ giác có thể nội tiếp được đường tròn, điều kiện tiên quyết là tổng hai góc đối của nó phải bằng 180 độ. Trong trường hợp hình thoi, điều này chỉ xảy ra khi nó là hình vuông.
