Mệnh đề là một câu khẳng định có tính chất hoặc đúng, hoặc sai, nhưng không thể đồng thời cả hai. Trong toán học, khái niệm Mệnh đề đúng đóng vai trò nền tảng cho mọi suy luận và chứng minh. Một mệnh đề chỉ được coi là mệnh đề đúng nếu nó phản ánh chính xác một sự thật hoặc một quy luật đã được chứng minh.
Mệnh Đề Kéo Theo và Điều Kiện Cần, Đủ
Mệnh đề kéo theo có dạng “Nếu P thì Q,” ký hiệu là $P Rightarrow Q$. Trong đó, P và Q là hai mệnh đề. Mệnh đề $P Rightarrow Q$ chỉ sai khi P đúng và Q sai; trong mọi trường hợp khác, nó là mệnh đề đúng.
Ví dụ:
- P: “Số 4 là số chẵn.” (Mệnh đề đúng)
- Q: “Số 5 là số nguyên tố.” (Mệnh đề đúng)
Khi đó, $P Rightarrow Q$: “Nếu số 4 là số chẵn thì số 5 là số nguyên tố.” Đây là một mệnh đề đúng.
Điều kiện cần và đủ: Nếu $P Rightarrow Q$ là một mệnh đề đúng, ta nói P là điều kiện đủ để có Q, và Q là điều kiện cần để có P. Nếu cả $P Rightarrow Q$ và $Q Rightarrow P$ đều là mệnh đề đúng, ta nói P là điều kiện cần và đủ để có Q, ký hiệu là $P Leftrightarrow Q$ (P tương đương với Q).
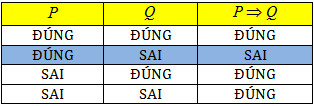
Bảng Chân Trị của Mệnh Đề Kéo Theo
Bảng chân trị giúp xác định tính đúng sai của mệnh đề kéo theo dựa trên tính đúng sai của các mệnh đề thành phần:
| P | Q | $P Rightarrow Q$ |
|---|---|---|
| Đúng | Đúng | Đúng |
| Đúng | Sai | Sai |
| Sai | Đúng | Đúng |
| Sai | Sai | Đúng |

Ứng Dụng trong Chứng Minh Phản Chứng
Chứng minh phản chứng là một kỹ thuật quan trọng trong toán học. Để chứng minh một mệnh đề $P Rightarrow Q$ là mệnh đề đúng, ta giả sử $P Rightarrow Q$ là sai, tức là P đúng và Q sai. Sau đó, ta sử dụng các lập luận logic để dẫn đến một mâu thuẫn. Từ mâu thuẫn này, ta kết luận rằng giả sử ban đầu là sai, và do đó $P Rightarrow Q$ là mệnh đề đúng.
Ví dụ: Chứng minh rằng nếu $n^2$ là số chẵn thì n là số chẵn.
- Giả sử: $n^2$ là số chẵn và n là số lẻ.
- Nếu n là số lẻ, thì $n = 2k + 1$ với k là số nguyên.
- Khi đó, $n^2 = (2k + 1)^2 = 4k^2 + 4k + 1 = 2(2k^2 + 2k) + 1$.
- Vậy $n^2$ là số lẻ. Điều này mâu thuẫn với giả thiết $n^2$ là số chẵn.
- Kết luận: Nếu $n^2$ là số chẵn thì n là số chẵn (đây là một mệnh đề đúng).
Bài Tập Vận Dụng
Để củng cố kiến thức về mệnh đề đúng, hãy cùng luyện tập với các bài tập sau:
Bài 1: Xét tính đúng sai của các mệnh đề sau:
a) Nếu tam giác ABC là tam giác đều thì tam giác ABC là tam giác cân.
b) Nếu 2 + 2 = 5 thì Paris là thủ đô của nước Anh.
c) Nếu số 6 chia hết cho 2 thì số 6 chia hết cho 4.
Bài 2: Cho P là mệnh đề đúng, Q là mệnh đề sai. Xác định tính đúng sai của các mệnh đề sau:
a) $P Rightarrow Q$
b) $Q Rightarrow P$
c) $overline{P} Rightarrow Q$
Bài 3: Chứng minh bằng phản chứng: Nếu a + b ≥ 2 thì hoặc a ≥ 1 hoặc b ≥ 1.
Hướng dẫn giải:
Bài 1:
a) Mệnh đề đúng. Tam giác đều là một trường hợp đặc biệt của tam giác cân.
b) Mệnh đề đúng. Vì mệnh đề P (2 + 2 = 5) là sai.
c) Mệnh đề sai. Số 6 chia hết cho 2 nhưng không chia hết cho 4.
Bài 2:
a) Sai. Vì P đúng và Q sai.
b) Đúng. Vì Q sai.
c) Sai. Vì $overline{P}$ sai và Q sai.
Bài 3:
Giả sử a + b ≥ 2 nhưng đồng thời a < 1 và b < 1.
Khi đó, a + b < 1 + 1 = 2. Điều này mâu thuẫn với giả thiết a + b ≥ 2.
Vậy, nếu a + b ≥ 2 thì hoặc a ≥ 1 hoặc b ≥ 1 (đây là một mệnh đề đúng).
Hiểu rõ về mệnh đề đúng và các ứng dụng của nó là rất quan trọng trong việc học toán và phát triển tư duy logic. Hãy luyện tập thường xuyên để nắm vững kiến thức này và áp dụng nó vào giải quyết các bài toán phức tạp hơn.

