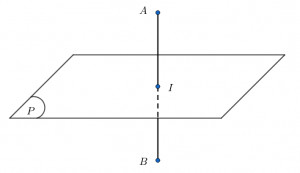
1. Định Nghĩa Mặt Phẳng Trung Trực
Trong không gian ba chiều, cho đoạn thẳng AB và điểm I là trung điểm của đoạn thẳng đó. Mặt phẳng (P) được gọi là Mặt Phẳng Trung Trực Của đoạn Thẳng Ab nếu nó đi qua điểm I và vuông góc với đường thẳng AB. Nói cách khác, mặt phẳng trung trực (P) chia đoạn thẳng AB thành hai phần bằng nhau và vuông góc với nó tại trung điểm I.
Hình ảnh minh họa mặt phẳng trung trực của đoạn thẳng AB, thể hiện rõ điểm I là trung điểm và mặt phẳng (P) vuông góc với AB.
2. Tính Chất Quan Trọng Của Mặt Phẳng Trung Trực
Mọi điểm nằm trên mặt phẳng trung trực của một đoạn thẳng đều cách đều hai đầu mút của đoạn thẳng đó. Tính chất này là một trong những đặc điểm quan trọng nhất giúp nhận biết và xác định mặt phẳng trung trực. Nếu một điểm M nằm trên mặt phẳng trung trực của đoạn thẳng AB, thì MA = MB.
Hình ảnh trực quan minh họa tính chất cách đều của mặt phẳng trung trực, giúp người đọc dễ hình dung và ghi nhớ.
3. Phương Pháp Viết Phương Trình Mặt Phẳng Trung Trực
Để viết phương trình mặt phẳng trung trực của đoạn thẳng AB trong không gian Oxyz, ta thực hiện theo các bước sau:
- Bước 1: Xác định tọa độ trung điểm I của đoạn thẳng AB. Tọa độ điểm I được tính bằng công thức: I ( (xA + xB)/2 ; (yA + yB)/2 ; (zA + zB)/2 ).
- Bước 2: Tìm vectơ chỉ phương của đường thẳng AB, chính là vectơ pháp tuyến của mặt phẳng trung trực (P). Vectơ AB được tính bằng công thức: $overrightarrow{AB}$ = (xB – xA ; yB – yA ; zB – zA).
- Bước 3: Viết phương trình mặt phẳng (P) đi qua điểm I và nhận vectơ $overrightarrow{AB}$ làm vectơ pháp tuyến. Phương trình tổng quát của mặt phẳng (P) có dạng: A(x – xI) + B(y – yI) + C(z – zI) = 0, trong đó (A; B; C) là tọa độ của vectơ $overrightarrow{AB}$.
Ví dụ 1: Cho hai điểm A(1; 2; 3) và B(3; 4; 1). Hãy viết phương trình mặt phẳng trung trực của đoạn thẳng AB.
Giải:
- Tìm tọa độ trung điểm I của AB: I((1+3)/2; (2+4)/2; (3+1)/2) => I(2; 3; 2).
- Tìm vectơ AB: $overrightarrow{AB}$ = (3-1; 4-2; 1-3) = (2; 2; -2).
- Viết phương trình mặt phẳng (P): 2(x – 2) + 2(y – 3) – 2(z – 2) = 0 <=> 2x + 2y – 2z – 6 = 0 <=> x + y – z – 3 = 0.
Vậy, phương trình mặt phẳng trung trực của đoạn thẳng AB là: x + y – z – 3 = 0.
Ví dụ 2: Trong không gian Oxyz, cho A(0; 1; -1) và B(2; -1; 1). Mặt phẳng trung trực của đoạn thẳng AB có phương trình là:
A. x – y + z = 0
B. x – y + z – 1 = 0
C. x + y – z = 0
D. x + y – z – 1 = 0
Giải:
- Trung điểm I của AB có tọa độ là I(1; 0; 0).
- Vectơ $overrightarrow{AB}$ = (2; -2; 2)
Phương trình mặt phẳng trung trực của AB là:
$2(x-1) -2(y-0) + 2(z-0) = 0$
$Leftrightarrow 2x – 2 – 2y + 2z = 0$
$Leftrightarrow x – y + z – 1 = 0$
Chọn đáp án B.
4. Bài Tập Vận Dụng
Bài 1: Cho A(2; -1; 0) và B(4; 1; -2). Viết phương trình mặt phẳng trung trực của đoạn thẳng AB.
Bài 2: Tìm phương trình mặt phẳng trung trực của đoạn thẳng AB, biết A(1; 0; 2) và B(-1; 2; 4).
Bài 3: Trong không gian Oxyz, cho điểm A(1; 2; -3) và B(3; -2; 1). Viết phương trình mặt phẳng (P) là mặt phẳng trung trực của đoạn thẳng AB.
Hình ảnh minh họa bài tập, giúp học sinh hình dung rõ hơn về cách áp dụng kiến thức vào giải bài tập.
Bài 4: Cho hai điểm A(1; -2; 3) và B(3; 4; -1). Xác định phương trình của mặt phẳng trung trực của đoạn thẳng AB.
Hình ảnh minh họa một ví dụ cụ thể về mặt phẳng trung trực, giúp người học dễ dàng liên hệ với bài toán thực tế.
Bài 5: Viết phương trình mặt phẳng trung trực của đoạn thẳng AB, biết A(2; 0; -1) và B(0; -2; 1).
Hình ảnh minh họa bài toán với các điểm M, N, P, giúp người học có cái nhìn đa dạng hơn về ứng dụng của mặt phẳng trung trực.
5. Ứng Dụng Của Mặt Phẳng Trung Trực
Mặt phẳng trung trực có nhiều ứng dụng quan trọng trong hình học và các lĩnh vực liên quan, bao gồm:
- Tìm tâm đường tròn ngoại tiếp tam giác: Trong không gian, giao của ba mặt phẳng trung trực của ba cạnh của một tam giác chính là tâm của đường tròn ngoại tiếp tam giác đó.
- Xây dựng các hình đối xứng: Mặt phẳng trung trực được sử dụng để tạo ra các hình đối xứng qua mặt phẳng.
- Giải quyết các bài toán liên quan đến khoảng cách: Tính chất cách đều của mặt phẳng trung trực giúp giải quyết các bài toán liên quan đến khoảng cách từ một điểm đến hai điểm khác.
Nắm vững kiến thức về mặt phẳng trung trực của đoạn thẳng AB sẽ giúp bạn giải quyết nhiều bài toán hình học không gian một cách hiệu quả. Chúc các bạn học tốt!