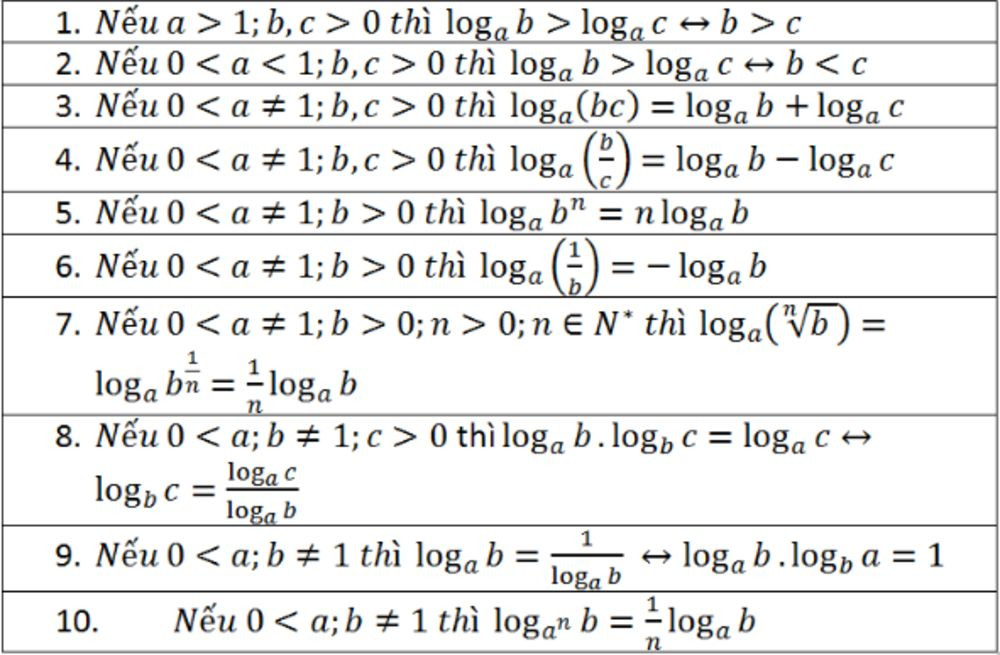Logarit là một khái niệm toán học quan trọng, xuất hiện xuyên suốt chương trình THPT và cả trong các kỳ thi quan trọng. Việc nắm vững các công thức logarit là yếu tố then chốt để giải quyết các bài toán liên quan. Bài viết này sẽ cung cấp một cái nhìn toàn diện về logarit, từ định nghĩa cơ bản đến các công thức nâng cao và ứng dụng thực tế.
Logarit Là Gì?
Logarit là phép toán nghịch đảo của lũy thừa. Hiểu một cách đơn giản, logarit của một số là số mũ mà cơ số (một giá trị cố định) cần được nâng lên để tạo ra số đó.
Ví dụ:
- 2³ = 8 (2 lũy thừa 3 bằng 8)
- log₂8 = 3 (logarit cơ số 2 của 8 bằng 3)
Phép toán logarit giúp chúng ta giải quyết các bài toán liên quan đến lũy thừa một cách dễ dàng hơn, đặc biệt trong các trường hợp số mũ chưa biết.
Tính Chất Của Logarit
Các tính chất của logarit là nền tảng để biến đổi và đơn giản hóa các biểu thức logarit. Dưới đây là một số tính chất quan trọng:
- logₐ1 = 0 (Logarit cơ số a của 1 luôn bằng 0)
- logₐa = 1 (Logarit cơ số a của a luôn bằng 1)
- logₐ(xy) = logₐx + logₐy (Logarit của một tích bằng tổng các logarit)
- logₐ(x/y) = logₐx – logₐy (Logarit của một thương bằng hiệu các logarit)
- *logₐ(xⁿ) = nlogₐx** (Logarit của một lũy thừa)
Các Công Thức Logarit Quan Trọng
Dưới đây là bảng tổng hợp các công thức logarit đầy đủ và chi tiết, bao gồm cả công thức lũy thừa, phép toán, đổi cơ số và đạo hàm.
Công Thức Logarit Cơ Bản
Công Thức Lũy Thừa Logarit
Công Thức Logarit và Các Phép Toán
Công Thức Phép Đổi Cơ Số
Công Thức Đạo Hàm Logarit
- Đạo hàm logarit hàm cơ bản:
- (logₐx)’ = 1/(x*ln(a))
- (ln(x))’ = 1/x
- Đạo hàm logarit hàm hợp:
Quy Tắc Logarit Lũy Thừa và Tích
- Quy tắc logarit lũy thừa: logₐ(b^α) = αlogₐb (với a, b > 0 và a ≠ 1)
- Quy tắc logarit của một tích: logₐ(bc) = logₐb + logₐc (với a, b, c > 0 và a ≠ 1)
Cách Tìm Logarit
Tìm Logarit Nhanh Bằng Bảng Logarit
Bảng logarit là một công cụ hữu ích để tính toán nhanh các phép nhân và chia số lớn. Để sử dụng bảng logarit hiệu quả, cần:
- Tìm đúng giá trị ô: Xác định giao điểm của hàng và cột tương ứng.
- Chọn đúng bảng: Sử dụng bảng logarit thập phân (cơ số 10) cho các phép tính thông thường.
- Tìm tiền tố: Xác định phần nguyên của logarit (đặc trưng) và phần thập phân (mantissa).
- Tìm phần nguyên: Đếm số chữ số của số thập phân và trừ đi 1.
- Tìm số chính xác: Sử dụng cột nhỏ hơn ở bên ngoài bảng để tìm giá trị chính xác hơn.
Tìm Logarit Nâng Cao
Để giải các phương trình logarit phức tạp, cần:
- Hiểu rõ định nghĩa logarit: Nắm vững mối quan hệ giữa logarit và lũy thừa.
- Xác định đặc tính của số: Phân tích số cần tính logarit.
- Sử dụng đúng bảng logarit: Chọn bảng phù hợp với cơ số của logarit.
- Tra bảng cẩn thận: Xác định giao điểm giữa hàng và cột để tìm giá trị logarit.
- Sử dụng bảng phụ: Áp dụng bảng phụ để tính toán chính xác hơn.
- Thêm đặc tính và mantissa: Kết hợp phần nguyên và phần thập phân để có kết quả cuối cùng.
Lưu Ý Khi Học Công Thức Logarit
- Phân biệt hàm mũ và logarit: Nhận diện sự khác biệt giữa phương trình logarit và phương trình mũ.
- Ghi nhớ thành phần: Nắm vững các thành phần của công thức logarit (cơ số, đối số, log).
- Phân biệt các loại logarit: Hiểu rõ sự khác nhau giữa logarit thập phân, logarit tự nhiên và các loại logarit khác.
Các Dạng Bài Tập Logarit Thường Gặp
- So sánh biểu thức chứa logarit: Sử dụng tính chất và công thức logarit để đơn giản hóa và so sánh.
- Biểu diễn một logarit qua các logarit đã cho: Áp dụng các tính chất logarit để tách và thay thế các biểu thức.
- Rút gọn biểu thức logarit: Chuyển đổi về cùng cơ số và rút gọn theo thứ tự phép tính.
Nắm vững các công thức và kỹ năng giải bài tập logarit sẽ giúp bạn tự tin hơn trong học tập và các kỳ thi quan trọng. Hãy luyện tập thường xuyên và tham khảo thêm các nguồn tài liệu uy tín để nâng cao kiến thức của mình.