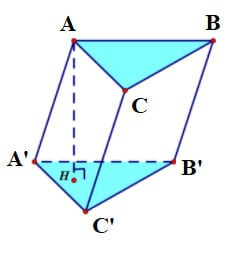
Hình lăng trụ là một khái niệm quan trọng trong hình học không gian. Để hiểu rõ hơn về lăng trụ tam giác đều và mối liên hệ của nó với lăng trụ đứng, chúng ta sẽ đi vào chi tiết các định nghĩa và tính chất liên quan.
Định nghĩa hình lăng trụ
Hình lăng trụ là một khối đa diện được tạo thành từ hai đáy là các đa giác bằng nhau, song song với nhau và các mặt bên là các hình bình hành.
Lăng trụ tam giác đều là gì?
Lăng trụ tam giác đều là một hình lăng trụ có hai mặt đáy là tam giác đều. Tuy nhiên, điều này không tự động khẳng định nó là lăng trụ đứng.
Lăng trụ đứng là gì?
Lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với mặt đáy. Điều này có nghĩa là các mặt bên của lăng trụ đứng là các hình chữ nhật.
Vậy lăng trụ tam giác đều có phải lăng trụ đứng không?
Câu trả lời là: Lăng trụ tam giác đều là lăng trụ đứng nếu các cạnh bên của nó vuông góc với mặt đáy là tam giác đều. Khi đó, các mặt bên của lăng trụ tam giác đều sẽ là các hình chữ nhật bằng nhau. Nếu các cạnh bên không vuông góc với mặt đáy, thì đó là lăng trụ tam giác đều nhưng không phải lăng trụ đứng.
Các dạng hình lăng trụ khác
Ngoài lăng trụ tam giác đều và lăng trụ đứng, còn có một số dạng lăng trụ khác:
- Lăng trụ đều: Là lăng trụ đứng có đáy là đa giác đều.
- Hình hộp: Là hình lăng trụ có đáy là hình bình hành.
- Hình hộp đứng: Là hình lăng trụ đứng có đáy là hình bình hành.
- Hình hộp chữ nhật: Là hình hộp đứng có đáy là hình chữ nhật.
- Hình lập phương: Là hình lăng trụ đứng có đáy là hình vuông và các mặt bên là hình vuông.
Công thức tính thể tích lăng trụ đứng
Thể tích của lăng trụ đứng được tính bằng công thức:
V = B.h
Trong đó:
- V: Thể tích khối lăng trụ
- B: Diện tích đáy
- h: Chiều cao của lăng trụ (khoảng cách giữa hai đáy)
Bài tập ví dụ
Bài 1: Cho hình lăng trụ đứng ABC.A′B′C′ có đáy là tam giác đều cạnh a. Biết mặt phẳng (A’BC) tạo với đáy một góc 60°. Tính thể tích khối lăng trụ.
Giải:
- Diện tích đáy của lăng trụ là S = (a²√3)/4
- Chiều cao của lăng trụ là h = AA’
- Góc giữa (A’BC) và đáy là góc giữa A’H và AH, với H là trung điểm BC.
- Tính AH = (a√3)/2
- Suy ra A’H = AH tan(60°) = (a√3)/2 √3 = (3a)/2
- Vậy thể tích lăng trụ là V = S h = ((a²√3)/4) ((3a)/2) = (3a³√3)/8
Bài 2: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a, đường chéo của mặt bên ABB’A’ là AB’ = a√2. Tính thể tích của khối lăng trụ.
Giải:
- Vì là lăng trụ đứng, nên AA’ vuông góc với đáy ABC.
- Tam giác ABB’ vuông tại A, ta có BB’ = √(AB’² – AB²) = √(2a² – a²) = a
- Diện tích đáy ABC là (a²√3)/4
- Thể tích lăng trụ là V = Sđáy chiều cao = ((a²√3)/4) a = (a³√3)/4
Kết luận:
Lăng trụ tam giác đều là lăng trụ đứng khi các cạnh bên vuông góc với mặt đáy. Việc hiểu rõ định nghĩa và tính chất của các loại lăng trụ giúp giải quyết các bài toán hình học không gian một cách chính xác và hiệu quả.