Lăng trụ tam giác đều là một khái niệm quan trọng trong hình học không gian. Để hiểu rõ hơn về loại hình này, chúng ta cần xem xét các đặc điểm, tính chất và công thức liên quan. Câu hỏi đặt ra là “Lăng Trụ Tam Giác đều Có đứng Không?” Bài viết này sẽ giải đáp thắc mắc đó và cung cấp thông tin chi tiết về lăng trụ tam giác đều.
Lăng Trụ Tam Giác Đều Là Gì?
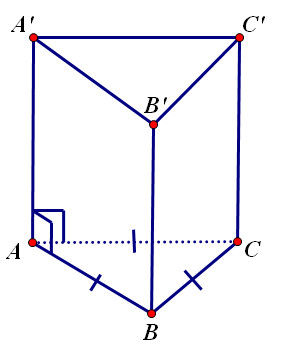
Lăng trụ tam giác đều là một hình lăng trụ có hai đáy là hai tam giác đều bằng nhau và các mặt bên là các hình chữ nhật. Đặc điểm quan trọng là các mặt bên này vuông góc với mặt đáy, tạo thành một hình “đứng”.
Ảnh: Mô tả hình lăng trụ tam giác đều với đáy là tam giác đều và các mặt bên là hình chữ nhật, minh họa trực quan về hình dạng và cấu trúc của hình học này.
Tính Chất Quan Trọng Của Lăng Trụ Tam Giác Đều
Để trả lời câu hỏi “lăng trụ tam giác đều có đứng không?”, ta cần xem xét các tính chất sau:
- Hai đáy là tam giác đều: Hai mặt đáy của lăng trụ là hai tam giác đều hoàn toàn giống nhau.
- Các cạnh đáy bằng nhau: Tất cả các cạnh của tam giác đáy đều có độ dài bằng nhau.
- Các mặt bên là hình chữ nhật: Ba mặt bên của lăng trụ là các hình chữ nhật có kích thước bằng nhau.
- Mặt bên vuông góc với đáy: Đây là tính chất quan trọng nhất để xác định xem lăng trụ có “đứng” hay không. Trong lăng trụ tam giác đều, các mặt bên luôn vuông góc với mặt đáy. Điều này có nghĩa là các cạnh bên (chiều cao của lăng trụ) vuông góc với mặt phẳng chứa tam giác đáy.
Vậy, câu trả lời là: Có, lăng trụ tam giác đều là hình lăng trụ đứng. Tính chất các mặt bên vuông góc với đáy là yếu tố then chốt để khẳng định điều này.
Công Thức Tính Thể Tích và Diện Tích
Để hiểu rõ hơn về lăng trụ tam giác đều, chúng ta cần nắm vững các công thức tính toán liên quan:
Thể Tích
Thể tích (V) của lăng trụ tam giác đều được tính bằng công thức:
V = S.h
Trong đó:
- S là diện tích đáy (tam giác đều)
- h là chiều cao của lăng trụ (khoảng cách giữa hai đáy)
Diện tích tam giác đều có cạnh a là: S = (a²√3) / 4
Vậy, công thức thể tích có thể viết lại là:
V = (a²√3) / 4 * h
Ảnh: Biểu diễn công thức tính thể tích khối lăng trụ tam giác đều, V = S.h, trong đó S là diện tích đáy và h là chiều cao.
Diện Tích Xung Quanh
Diện tích xung quanh (Sxq) của lăng trụ tam giác đều là tổng diện tích của ba mặt bên hình chữ nhật:
Sxq = P.h
Trong đó:
- P là chu vi đáy (tam giác đều)
- h là chiều cao của lăng trụ
Chu vi tam giác đều có cạnh a là: P = 3a
Vậy, công thức diện tích xung quanh là:
Sxq = 3a.h
Diện Tích Toàn Phần
Diện tích toàn phần (Stp) của lăng trụ tam giác đều là tổng của diện tích xung quanh và diện tích hai đáy:
Stp = Sxq + 2S
Trong đó:
- Sxq là diện tích xung quanh
- S là diện tích đáy (tam giác đều)
Vậy, công thức diện tích toàn phần là:
Stp = 3a.h + 2 * (a²√3) / 4 = 3ah + (a²√3) / 2
Bài Tập Ví Dụ
Để củng cố kiến thức, chúng ta hãy xem xét một số bài tập ví dụ:
Ví dụ 1: Một lăng trụ tam giác đều có cạnh đáy là 5cm và chiều cao là 10cm. Tính thể tích của lăng trụ.
Giải:
- Diện tích đáy: S = (5²√3) / 4 = (25√3) / 4 cm²
- Thể tích: V = S.h = (25√3) / 4 * 10 = (250√3) / 4 = (125√3) / 2 cm³
Ví dụ 2: Một lăng trụ tam giác đều có cạnh đáy là 4cm và chiều cao là 7cm. Tính diện tích xung quanh và diện tích toàn phần của lăng trụ.
Giải:
- Chu vi đáy: P = 3 * 4 = 12 cm
- Diện tích xung quanh: Sxq = P.h = 12 * 7 = 84 cm²
- Diện tích đáy: S = (4²√3) / 4 = 4√3 cm²
- Diện tích toàn phần: Stp = Sxq + 2S = 84 + 2 * 4√3 = 84 + 8√3 cm²
Ứng Dụng Thực Tế
Lăng trụ tam giác đều không chỉ là một khái niệm hình học trừu tượng, mà còn có nhiều ứng dụng thực tế trong kiến trúc, xây dựng và thiết kế. Ví dụ, chúng có thể được sử dụng để tạo ra các cấu trúc mái nhà, các bộ phận của máy móc, hoặc các vật dụng trang trí.
Kết Luận
Qua bài viết này, chúng ta đã làm rõ khái niệm lăng trụ tam giác đều và khẳng định rằng lăng trụ tam giác đều là hình lăng trụ đứng. Chúng ta cũng đã tìm hiểu về các tính chất, công thức tính toán và ứng dụng thực tế của loại hình này. Hy vọng rằng thông tin này sẽ giúp bạn hiểu sâu hơn về hình học không gian và ứng dụng nó vào thực tiễn.