Trong vật lý và kỹ thuật, đặc biệt trong các lĩnh vực liên quan đến dao động và sóng, Ký Hiệu Tần Số Góc đóng vai trò vô cùng quan trọng. Vậy tần số góc là gì? Ký hiệu tần số góc là gì? Bài viết này sẽ cung cấp một cái nhìn toàn diện về khái niệm này, các ứng dụng thực tế và các công thức liên quan.
Tần Số Góc Là Gì?
Tần số góc (hay còn gọi là tốc độ góc) là một đại lượng vật lý mô tả tốc độ thay đổi của góc trong một chuyển động tròn hoặc dao động điều hòa. Nó cho biết góc mà một vật quét được trong một đơn vị thời gian.
Ký Hiệu Tần Số Góc
Ký hiệu tần số góc thường được sử dụng là chữ cái Hy Lạp omega: ω. Đơn vị đo của tần số góc là radian trên giây (rad/s).
Mối Quan Hệ Giữa Tần Số Góc và Tần Số
Tần số (f) là số lần một hiện tượng lặp lại trong một đơn vị thời gian (thường là giây). Tần số góc (ω) và tần số (f) có mối quan hệ mật thiết với nhau, được biểu diễn qua công thức:
ω = 2πf
Trong đó:
- ω: Tần số góc (rad/s)
- π: Hằng số Pi (≈ 3.14159)
- f: Tần số (Hz)
Công thức này cho thấy tần số góc tỉ lệ thuận với tần số, và hệ số tỉ lệ là 2π.
Công Thức Tính Tần Số Góc
Để tính ký hiệu tần số góc, ta có thể sử dụng một số công thức tùy thuộc vào thông tin đã biết:
-
Từ Tần Số (f):
ω = 2πf
-
Từ Chu Kỳ (T):
ω = 2π/T (Vì f = 1/T)
-
Trong Dao Động Điều Hòa:
Nếu biết phương trình dao động điều hòa: x(t) = Acos(ωt + φ), thì ω chính là tần số góc.
Ứng Dụng Của Tần Số Góc
Tần số góc được sử dụng rộng rãi trong nhiều lĩnh vực khoa học và kỹ thuật, bao gồm:
- Cơ học: Mô tả chuyển động quay của các vật thể, ví dụ như bánh xe, động cơ.
- Điện tử học: Phân tích các mạch điện xoay chiều (AC), đặc biệt là các mạch RLC.
- Vật lý sóng: Mô tả các sóng cơ học (như sóng âm) và sóng điện từ (như ánh sáng).
- Điều khiển học: Thiết kế các hệ thống điều khiển, ví dụ như hệ thống điều khiển tốc độ động cơ.
- Xử lý tín hiệu: Phân tích và xử lý các tín hiệu thời gian, ví dụ như tín hiệu âm thanh, tín hiệu hình ảnh.
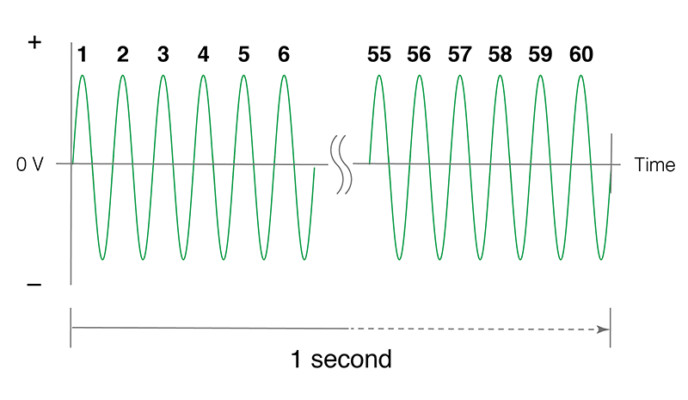
Minh họa mối quan hệ giữa tần số và chu kỳ dao động.
Ví Dụ Minh Họa
Ví dụ 1: Một vật dao động điều hòa với tần số 5 Hz. Tính tần số góc của dao động này.
- Giải: Sử dụng công thức ω = 2πf, ta có:
ω = 2 3.14159 5 = 31.4159 rad/s
Ví dụ 2: Một động cơ quay với tốc độ 1200 vòng/phút (RPM). Tính tần số góc của động cơ này.
- Giải: Đầu tiên, chuyển đổi RPM sang vòng/giây (Hz): 1200 RPM = 1200/60 = 20 Hz. Sau đó, sử dụng công thức ω = 2πf, ta có:
ω = 2 3.14159 20 = 125.664 rad/s
Phân Biệt Tần Số Góc (ω) và Tần Số (f)
Nhiều người thường nhầm lẫn giữa tần số góc (ω) và tần số (f). Dưới đây là bảng so sánh để làm rõ sự khác biệt:
| Đặc điểm | Tần số (f) | Tần số góc (ω) |
|---|---|---|
| Định nghĩa | Số lần lặp lại của một hiện tượng trong 1 giây | Tốc độ thay đổi của góc trong 1 giây |
| Ký hiệu | f | ω |
| Đơn vị | Hertz (Hz) | Radian trên giây (rad/s) |
| Mối quan hệ | f = ω / (2π) | ω = 2πf |
| Ứng dụng | Đo lường số lần lặp lại | Mô tả chuyển động tròn hoặc dao động điều hòa |

Các Yếu Tố Ảnh Hưởng Đến Tần Số Góc
Trong các hệ thống vật lý, tần số góc có thể bị ảnh hưởng bởi nhiều yếu tố khác nhau, ví dụ như:
- Độ cứng của lò xo (k): Trong hệ lò xo – khối lượng, tần số góc tỉ lệ thuận với căn bậc hai của độ cứng lò xo.
- Khối lượng (m): Trong hệ lò xo – khối lượng, tần số góc tỉ lệ nghịch với căn bậc hai của khối lượng.
- Điện dung (C) và Độ tự cảm (L): Trong mạch LC, tần số góc tỉ lệ nghịch với căn bậc hai của tích LC.
Công thức tính tần số và các đại lượng liên quan.
Tần Số Góc Trong Các Lĩnh Vực Khác Nhau
Tần số góc là một khái niệm đa năng, được áp dụng trong nhiều lĩnh vực khác nhau. Dưới đây là một số ví dụ cụ thể:
-
Âm Thanh: Tần số góc của sóng âm thanh quyết định cao độ của âm thanh đó. Tần số góc càng cao, âm thanh càng cao.
-
Ánh Sáng: Tần số góc của sóng ánh sáng quyết định màu sắc của ánh sáng đó. Tần số góc càng cao, ánh sáng càng có màu thiên về tím và xanh.
-
Điện: Trong mạch điện xoay chiều, tần số góc quyết định trở kháng của các phần tử như cuộn cảm và tụ điện.
-
Cơ Học: Tần số góc được sử dụng để mô tả tốc độ quay của các vật thể, như trục động cơ, bánh xe, và các bộ phận máy móc khác.
Kết Luận
Ký hiệu tần số góc (ω) là một khái niệm quan trọng trong vật lý và kỹ thuật, giúp mô tả tốc độ thay đổi của góc trong chuyển động tròn và dao động điều hòa. Việc hiểu rõ định nghĩa, công thức tính toán và ứng dụng của tần số góc sẽ giúp bạn nắm vững kiến thức về dao động, sóng và các hệ thống vật lý liên quan. Hy vọng bài viết này đã cung cấp cho bạn cái nhìn tổng quan và chi tiết về ký hiệu tần số góc.