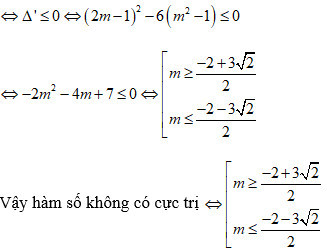Bài viết này trình bày chi tiết cách tìm tham số m để một hàm số bậc ba Không Có Cực Trị, một dạng toán quan trọng trong chương trình Toán lớp 12 và thường xuất hiện trong các kỳ thi. Chúng ta sẽ đi sâu vào lý thuyết, phương pháp giải, và các ví dụ minh họa có lời giải chi tiết.
Hàm số bậc ba và điều kiện không có cực trị
Xét hàm số bậc ba có dạng:
y = ax³ + bx² + cx + d (với a ≠ 0)
Để hàm số này không có cực trị, đạo hàm bậc nhất của nó (y’) phải vô nghiệm hoặc có nghiệm kép. Ta có:
y’ = 3ax² + 2bx + c
Vậy, điều kiện để hàm số không có cực trị là phương trình y’ = 0 vô nghiệm hoặc có nghiệm kép. Điều này tương đương với việc biệt thức delta (Δ) của phương trình bậc hai y’ = 0 nhỏ hơn hoặc bằng 0.
Δ’ ≤ 0 ⇔ b² – 3ac ≤ 0
Các bước giải bài toán tìm m để hàm số không có cực trị
- Tính đạo hàm bậc nhất (y’) của hàm số.
- Tìm điều kiện để phương trình y’ = 0 vô nghiệm hoặc có nghiệm kép: Tính Δ’ = b² – 3ac và đặt Δ’ ≤ 0.
- Giải bất phương trình Δ’ ≤ 0 để tìm ra khoảng giá trị của m.
- Kết luận: Giá trị của m tìm được là giá trị cần tìm để hàm số không có cực trị.
Ví dụ minh họa
Để hiểu rõ hơn, chúng ta cùng xét một số ví dụ cụ thể:
Ví dụ 1:
Tìm tất cả các giá trị của m để hàm số y = x³ + mx² + 3x + 1 không có cực trị.
Giải:
- Tính đạo hàm: y’ = 3x² + 2mx + 3
- Điều kiện không có cực trị: Δ’ = m² – 9 ≤ 0
- Giải bất phương trình: -3 ≤ m ≤ 3
- Kết luận: Hàm số không có cực trị khi -3 ≤ m ≤ 3.
Ví dụ 2:
Tìm m để hàm số y = -x³ + 3x² – (m+1)x + 2 không có cực trị.
Giải:
- Tính đạo hàm: y’ = -3x² + 6x – (m+1)
- Điều kiện không có cực trị: Δ’ = 9 – 3(m+1) ≤ 0
- Giải bất phương trình: 6 – 3m ≤ 0 => m ≥ 2
- Kết luận: Hàm số không có cực trị khi m ≥ 2.
Bài tập tự luyện
Để củng cố kiến thức, bạn có thể tự giải các bài tập sau:
- Tìm m để hàm số y = x³ – 3mx² + 3x – 1 không có cực trị.
- Tìm m để hàm số y = (m-1)x³ + 3x² + (2m+1)x – 5 không có cực trị.
Các lưu ý quan trọng
- Kiểm tra điều kiện a ≠ 0: Đảm bảo hệ số của x³ khác 0, vì nếu không, hàm số không còn là hàm bậc ba.
- Xét các trường hợp đặc biệt: Trong một số bài toán, có thể cần xét riêng các trường hợp đặc biệt (ví dụ: khi m = 1) để đảm bảo tính chính xác của kết quả.
Mở rộng kiến thức
Ngoài hàm bậc ba, bạn có thể áp dụng các phương pháp tương tự để xét tính cực trị của các hàm số khác, như hàm bậc bốn trùng phương.
Qua hình ảnh minh họa, ta thấy đồ thị hàm số bậc ba không có cực trị khi y’ = 0 có nghiệm kép hoặc vô nghiệm, dẫn đến Δ’ ≤ 0.
Ví dụ 3:
Cho hàm số y = -2x³+(2m – 1)x²-(m² – 1)x – 2. Tìm tất cả các giá trị của tham số m để hàm số đã cho sẽ không có cực trị.
Giải:
Tính đạo hàm: y’ = -6x² + 2(2m – 1)x – (m² – 1)
Để hàm số không có cực trị, phương trình y’ = 0 phải vô nghiệm hoặc có nghiệm kép, tức là Δ’ ≤ 0
Δ’ = (2m-1)² – 6(m²-1) ≤ 0
<=> 4m² – 4m + 1 – 6m² + 6 ≤ 0
<=> -2m² – 4m + 7 ≤ 0
<=> 2m² + 4m – 7 ≥ 0
Giải bất phương trình trên ta được:
m ≤ (-2 – √18)/2 hoặc m ≥ (-2 + √18)/2
Vậy m ≤ -1 – (3√2)/2 hoặc m ≥ -1 + (3√2)/2
Ví dụ 4:
Tìm tất cả các giá trị của tham số m để hàm số không có cực trị.
Giải:
Xét m = 1, hàm số trở thành y = 3x² + x + 2. Đây là hàm số bậc hai nên luôn có 1 cực trị. Vậy m = 1 (loại).
Xét m ≠ 1: y’ = (m – 1)x² + 2(m + 2)x + m
Để hàm số không có cực trị thì phương trình y’ = 0 vô nghiệm hoặc có nghiệm kép.
Δ’ = (m+2)² – m(m-1) ≤ 0
<=> m² + 4m + 4 – m² + m ≤ 0
<=> 5m + 4 ≤ 0
<=> m ≤ -4/5
Kết hợp điều kiện m ≠ 1, ta có m ≤ -4/5.
Hình ảnh minh họa công thức tính Δ’ = (m+2)² – m(m-1) và việc giải bất phương trình Δ’ ≤ 0 để tìm giá trị m.
Kết luận
Việc tìm m để hàm số không có cực trị là một kỹ năng quan trọng trong giải toán. Bằng cách nắm vững lý thuyết, phương pháp giải, và thực hành với các ví dụ, bạn sẽ tự tin giải quyết các bài toán liên quan đến chủ đề này. Hãy nhớ rằng, việc hiểu rõ bản chất vấn đề và luyện tập thường xuyên là chìa khóa để thành công.