Khối lăng trụ là một hình hình học không gian quen thuộc, và trong số đó, Khối Lăng Trụ đều nổi bật với những đặc điểm và tính chất riêng biệt. Bài viết này sẽ cung cấp cho bạn một cái nhìn toàn diện về khối lăng trụ đều, từ định nghĩa cơ bản đến các công thức tính toán và ứng dụng thực tế.
Định Nghĩa và Tính Chất của Khối Lăng Trụ Đều
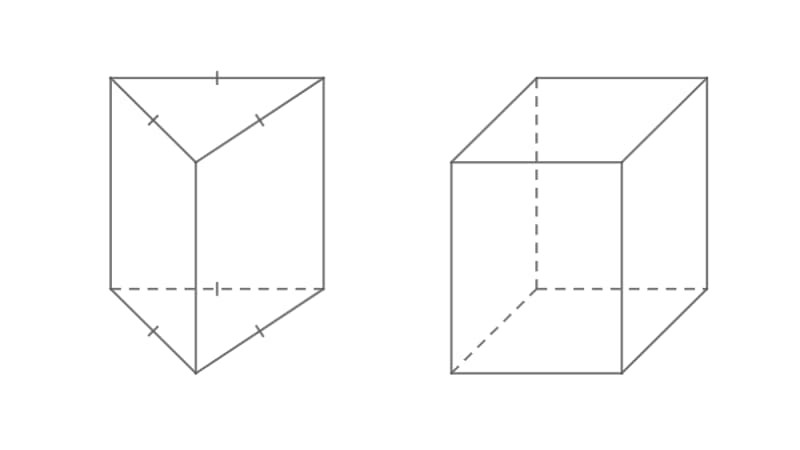
Khối lăng trụ đều là một trường hợp đặc biệt của khối lăng trụ đứng, với đáy là một đa giác đều. Điều này có nghĩa là tất cả các cạnh của đa giác đáy đều bằng nhau và tất cả các góc của đa giác đáy đều bằng nhau. Các mặt bên của khối lăng trụ đều là các hình chữ nhật bằng nhau và vuông góc với mặt đáy.
Hình ảnh minh họa khối lăng trụ tam giác đều, nhấn mạnh các cạnh đáy bằng nhau và các mặt bên là hình chữ nhật vuông góc với đáy.
Tính chất quan trọng của khối lăng trụ đều:
- Hai đáy là hai đa giác đều bằng nhau và nằm trên hai mặt phẳng song song.
- Các cạnh bên song song và bằng nhau, đồng thời vuông góc với mặt đáy.
- Các mặt bên là các hình chữ nhật bằng nhau.
Các Loại Khối Lăng Trụ Đều Phổ Biến
Dựa vào hình dạng của đa giác đáy, ta có các loại khối lăng trụ đều khác nhau:
- Khối lăng trụ tam giác đều: Đáy là tam giác đều.
- Khối lăng trụ tứ giác đều (hay hình hộp chữ nhật): Đáy là hình vuông.
- Khối lăng trụ ngũ giác đều: Đáy là ngũ giác đều.
- Và tương tự cho các đa giác đều khác.
Minh họa trực quan về sự đa dạng của các khối lăng trụ đứng, từ tam giác đến tứ giác và các hình phức tạp hơn.
Công Thức Tính Toán Liên Quan Đến Khối Lăng Trụ Đều
Để giải các bài toán liên quan đến khối lăng trụ đều, bạn cần nắm vững các công thức sau:
1. Diện Tích Xung Quanh (Sxq)
Diện tích xung quanh của khối lăng trụ đều bằng chu vi đáy nhân với chiều cao (độ dài cạnh bên):
Sxq = Pđáy * h
Trong đó:
Pđáy: Chu vi của đa giác đáy.h: Chiều cao của khối lăng trụ (độ dài cạnh bên).
Hình ảnh minh họa công thức tính diện tích xung quanh của hình lăng trụ, thể hiện mối quan hệ giữa chu vi đáy và chiều cao.
2. Diện Tích Toàn Phần (Stp)
Diện tích toàn phần của khối lăng trụ đều bằng diện tích xung quanh cộng với diện tích hai đáy:
Stp = Sxq + 2 * Sđáy
Trong đó:
Sđáy: Diện tích của đa giác đáy.
Công thức tính diện tích toàn phần, kết hợp diện tích xung quanh và diện tích hai đáy.
3. Thể Tích (V)
Thể tích của khối lăng trụ đều bằng diện tích đáy nhân với chiều cao:
V = Sđáy * h
Công thức đơn giản nhưng mạnh mẽ để tính thể tích của hình lăng trụ đứng, dựa trên diện tích đáy và chiều cao.
Ứng Dụng Thực Tế của Khối Lăng Trụ Đều
Khối lăng trụ đều xuất hiện rất nhiều trong cuộc sống hàng ngày và trong các lĩnh vực kỹ thuật, xây dựng:
- Kiến trúc: Các tòa nhà, cột trụ, mái nhà thường có hình dạng lăng trụ.
- Đóng gói: Nhiều sản phẩm được đóng gói trong các hộp hình lăng trụ để tối ưu hóa không gian.
- Cơ khí: Các chi tiết máy, trục, bánh răng có thể có hình dạng lăng trụ.
- Xây dựng: Các khối bê tông, dầm, xà thường có hình dạng lăng trụ.
Ứng dụng thực tế của hình lăng trụ trong kiến trúc và xây dựng, thể hiện tính ứng dụng cao trong đời sống.
Bài Tập Ví Dụ Về Khối Lăng Trụ Đều
Ví dụ 1: Cho khối lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và chiều cao bằng 2a. Tính thể tích của khối lăng trụ.
Giải:
Diện tích đáy (tam giác đều) là: Sđáy = (a^2 * √3) / 4
Thể tích khối lăng trụ là: V = Sđáy * h = ((a^2 * √3) / 4) * 2a = (a^3 * √3) / 2
Ví dụ 2: Một bể nước có dạng khối lăng trụ đứng đáy là hình vuông cạnh 2m, chiều cao 1.5m. Tính thể tích của bể nước.
Giải:
Diện tích đáy (hình vuông) là: Sđáy = 2m * 2m = 4 m^2
Thể tích bể nước là: V = Sđáy * h = 4 m^2 * 1.5m = 6 m^3
Phân Biệt Khối Lăng Trụ Đều với Các Loại Lăng Trụ Khác
Để hiểu rõ hơn về khối lăng trụ đều, cần phân biệt nó với các loại lăng trụ khác:
- Lăng trụ đứng: Các mặt bên vuông góc với đáy, nhưng đáy có thể là đa giác bất kỳ.
- Lăng trụ xiên: Các mặt bên không vuông góc với đáy.
- Lăng trụ đều: Là lăng trụ đứng và có đáy là đa giác đều.
So sánh trực quan giữa các loại hình lăng trụ khác nhau, giúp người đọc dễ dàng phân biệt và hiểu rõ hơn về đặc điểm của từng loại.
Kết Luận
Khối lăng trụ đều là một hình hình học quan trọng với nhiều ứng dụng trong thực tế. Việc nắm vững định nghĩa, tính chất và các công thức tính toán liên quan sẽ giúp bạn giải quyết các bài toán hình học không gian một cách dễ dàng và hiệu quả. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về khối lăng trụ đều.