Trong hình học không gian, việc xác định khoảng cách từ một điểm đến một mặt phẳng là một bài toán quan trọng. Bài viết này sẽ cung cấp định nghĩa, công thức tính toán và các phương pháp giải quyết bài toán này một cách chi tiết và dễ hiểu.
Định Nghĩa Khoảng Cách Từ Điểm Đến Mặt Phẳng
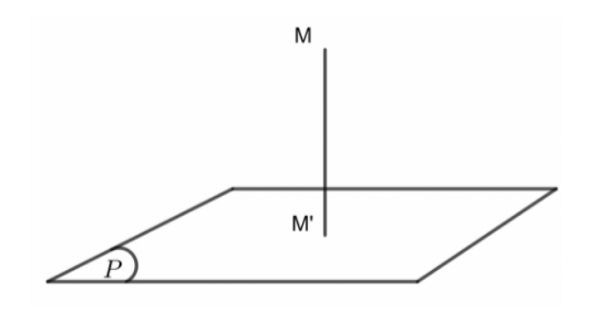
Khoảng cách từ một điểm M đến một mặt phẳng (P) là độ dài đoạn thẳng MH, trong đó H là hình chiếu vuông góc của điểm M trên mặt phẳng (P). Nói cách khác, MH là đoạn vuông góc hạ từ M xuống (P).
Ký hiệu: d(M,(P)) = MH
Công Thức Tính Khoảng Cách Từ Điểm Đến Mặt Phẳng Trong Hệ Tọa Độ Oxyz
Trong không gian tọa độ Oxyz, cho điểm M(x₀; y₀; z₀) và mặt phẳng (P) có phương trình tổng quát: ax + by + cz + d = 0. Khoảng cách từ điểm M đến mặt phẳng (P) được tính theo công thức sau:
d(M,(P)) =
Công thức này cho phép tính toán nhanh chóng khoảng cách khi biết tọa độ điểm và phương trình mặt phẳng.
Các Phương Pháp Tính Khoảng Cách Từ Điểm Đến Mặt Phẳng
Ngoài việc áp dụng công thức trực tiếp, có nhiều phương pháp khác để tính khoảng cách từ điểm đến mặt phẳng, tùy thuộc vào đặc điểm của bài toán.
Phương Pháp 1: Dựa Vào Định Nghĩa
Đây là phương pháp cơ bản nhất. Ta thực hiện các bước sau:
- Tìm hình chiếu vuông góc H của điểm M trên mặt phẳng (P).
- Tính độ dài đoạn thẳng MH, đây chính là khoảng cách cần tìm. Để tính MH, bạn có thể sử dụng công thức tính khoảng cách giữa hai điểm trong không gian.
Phương Pháp 2: Tính Khoảng Cách Gián Tiếp
Trong nhiều trường hợp, việc tìm hình chiếu trực tiếp của điểm M lên mặt phẳng (P) có thể phức tạp. Khi đó, ta có thể sử dụng phương pháp gián tiếp:
- Tìm một điểm N sao cho đường thẳng MN song song với mặt phẳng (P).
- Khi đó, khoảng cách từ M đến (P) bằng khoảng cách từ N đến (P): d(M, (P)) = d(N, (P)). Việc chọn điểm N thích hợp có thể giúp đơn giản hóa bài toán.
Phương Pháp 3: Sử Dụng Tam Giác Đồng Dạng
Phương pháp này thường được sử dụng khi có một điểm O cho trước và ta cần tính khoảng cách từ một điểm A khác đến mặt phẳng (P).
- Tìm giao điểm I của đường thẳng OA với mặt phẳng (P).
- Sử dụng định lý Ta-lét hoặc tính chất tam giác đồng dạng để thiết lập tỉ lệ thức giữa các khoảng cách: d(O,(P))/d(A,(P)) = OI/AI. Từ đó, suy ra khoảng cách d(A, (P)).
Ứng Dụng và Bài Tập Vận Dụng
Việc nắm vững lý thuyết và các phương pháp tính khoảng cách từ điểm đến mặt phẳng là rất quan trọng trong hình học không gian. Các bài tập vận dụng sẽ giúp củng cố kiến thức và rèn luyện kỹ năng giải toán.
Kết Luận
Bài viết đã trình bày một cách đầy đủ và chi tiết về khoảng cách từ một điểm đến một mặt phẳng, bao gồm định nghĩa, công thức và các phương pháp tính toán. Việc hiểu rõ và vận dụng linh hoạt các kiến thức này sẽ giúp bạn giải quyết các bài toán hình học không gian một cách hiệu quả.