Trong lĩnh vực khoa học dữ liệu và học máy, việc lựa chọn phương pháp đo khoảng cách phù hợp giữa các điểm dữ liệu là vô cùng quan trọng. Các phương pháp này được sử dụng rộng rãi trong các thuật toán như k-NN, UMAP, DBSCAN, và nhiều thuật toán khác. Bài viết này sẽ đi sâu vào một trong những phương pháp phổ biến nhất: Khoảng Cách Manhattan, hay còn gọi là khoảng cách L1.
1. Giới Thiệu về Khoảng Cách Manhattan
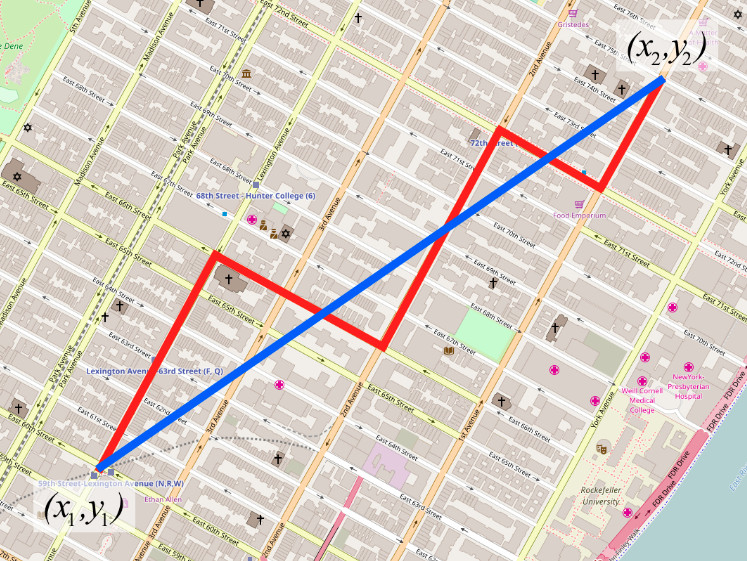
Khoảng cách Manhattan, còn được biết đến với tên gọi khoảng cách L1, Taxicab distance, hoặc City Block distance, là một cách đo khoảng cách giữa hai điểm trong không gian n chiều. Thay vì đo đường chim bay như khoảng cách Euclidean, khoảng cách Manhattan đo tổng độ dài các đoạn thẳng song song với các trục tọa độ.
Để dễ hình dung, hãy tưởng tượng bạn đang đi trong một thành phố với các con đường vuông góc nhau. Khoảng cách Manhattan chính là tổng quãng đường bạn phải đi để đến đích, đi theo các con đường có sẵn.
Công thức tính khoảng cách Manhattan giữa hai điểm x và y trong không gian k chiều:
D(x,y)=∑i=1k∣xi−yi∣D(x, y) = sum_{i=1}^k |x_i – y_i| D(x,y)=i=1∑k∣xi−yi∣
Trong đó:
xvàylà hai điểm trong không gian k chiều.xivàyilà tọa độ của điểmxvàytrên chiều thứi.|xi - yi|là giá trị tuyệt đối của hiệu giữa tọa độ của điểmxvàytrên chiều thứi.
Một biến thể khác của khoảng cách Manhattan là khoảng cách Canberra:
D(x,y)=∑i=1n∣xi−yi∣∣xi∣+∣yi∣D(x, y) = sum_{i=1}^n frac{|x_i – y_i|}{|x_i| + |y_i|} D(x,y)=i=1∑n∣xi∣+∣yi∣∣xi−yi∣
Khoảng cách Canberra tương tự như khoảng cách L1 Manhattan, nhưng có xét đến độ lớn của các vector.
2. Ưu Điểm và Nhược Điểm của Khoảng Cách Manhattan
Ưu điểm:
- Đơn giản và dễ hiểu: Công thức tính toán đơn giản, dễ dàng implement trong các ứng dụng thực tế.
- Ít bị ảnh hưởng bởi outliers: Do chỉ tính tổng giá trị tuyệt đối của hiệu, khoảng cách Manhattan ít bị ảnh hưởng bởi các điểm dữ liệu ngoại lệ so với khoảng cách Euclidean.
- Phù hợp với dữ liệu có tính chất rời rạc: Đặc biệt hiệu quả khi dữ liệu có tính chất rời rạc hoặc các chiều dữ liệu có ý nghĩa độc lập với nhau.
- Ứng dụng trong so sánh chuỗi: Khoảng cách Manhattan có thể được sử dụng như một string metric để so sánh sự khác biệt giữa các chuỗi.
Nhược điểm:
- Không phù hợp với dữ liệu liên tục: Trong trường hợp dữ liệu liên tục, khoảng cách Euclidean thường cho kết quả tốt hơn vì nó tính đến “đường chim bay” giữa các điểm.
- Phụ thuộc vào hệ tọa độ: Kết quả của khoảng cách Manhattan phụ thuộc vào hệ tọa độ được sử dụng. Nếu hệ tọa độ thay đổi, khoảng cách giữa các điểm cũng sẽ thay đổi.
- Không thể hiện hướng: Khoảng cách Manhattan chỉ đo độ lớn khác biệt giữa các điểm, không thể hiện hướng khác biệt.
3. Ứng Dụng của Khoảng Cách Manhattan
Khoảng cách Manhattan được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, bao gồm:
- Học máy:
- k-NN (k-Nearest Neighbors): Sử dụng khoảng cách Manhattan để tìm k điểm gần nhất với một điểm dữ liệu mới.
- Phân cụm: Sử dụng trong các thuật toán phân cụm như k-Means hoặc DBSCAN.
- Xử lý ảnh:
- So sánh ảnh: So sánh sự khác biệt giữa các ảnh bằng cách tính khoảng cách Manhattan giữa các pixel.
- Nhận dạng ký tự: Sử dụng để nhận dạng các ký tự viết tay hoặc in.
- Hệ thống khuyến nghị:
- Khuyến nghị sản phẩm: Dựa trên lịch sử mua hàng của người dùng, sử dụng khoảng cách Manhattan để tìm những người dùng có sở thích tương tự và khuyến nghị các sản phẩm mà họ đã mua.
- Tìm đường:
- Định vị GPS: Tính toán quãng đường đi ngắn nhất giữa hai địa điểm trong thành phố.
4. So Sánh với Các Phương Pháp Đo Khoảng Cách Khác
Để hiểu rõ hơn về khoảng cách Manhattan, chúng ta hãy so sánh nó với một số phương pháp đo khoảng cách phổ biến khác:
- Khoảng cách Euclidean:
- Tính “đường chim bay” giữa hai điểm.
- Phù hợp với dữ liệu liên tục và không bị ảnh hưởng bởi hệ tọa độ.
- Dễ bị ảnh hưởng bởi outliers.
- Khoảng cách Chebyshev:
- Tính độ lệch lớn nhất của hai vector theo trục tọa độ.
- Phù hợp với các bài toán tìm bước đi tối thiểu trong trò chơi hoặc điều khiển cần trục trong kho vận.
- Không có tính generalize tốt như Euclidean hay Cosine similarity.
- Cosine Similarity:
- Tính góc giữa hai vector.
- Phù hợp với dữ liệu đa chiều và không quá phụ thuộc vào độ lớn của vector.
- Không tận dụng độ lớn của vector, chỉ tính theo hướng.
- Khoảng cách Hamming:
- Tính số lượng giá trị khác nhau giữa hai vector.
- Phù hợp với dữ liệu categorical hoặc so sánh chuỗi binary.
- Khó áp dụng với hai vector có số chiều không tương đồng.
5. Kết Luận
Khoảng cách Manhattan là một phương pháp đo khoảng cách đơn giản, dễ hiểu và có nhiều ứng dụng thực tế. Việc lựa chọn phương pháp đo khoảng cách phù hợp phụ thuộc vào tính chất của dữ liệu và yêu cầu của bài toán. Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan về khoảng cách Manhattan và giúp bạn đưa ra quyết định tốt nhất cho dự án của mình.