Trong hình học không gian, việc xác định Khoảng Cách 2 đường Thẳng Chéo Nhau là một bài toán quan trọng. Bài viết này sẽ cung cấp định nghĩa chi tiết, các phương pháp tính toán hiệu quả, cùng với các bài tập minh họa có lời giải, giúp bạn nắm vững kiến thức và tự tin giải quyết các bài toán liên quan.
1. Định Nghĩa Khoảng Cách Giữa Hai Đường Thẳng Chéo Nhau
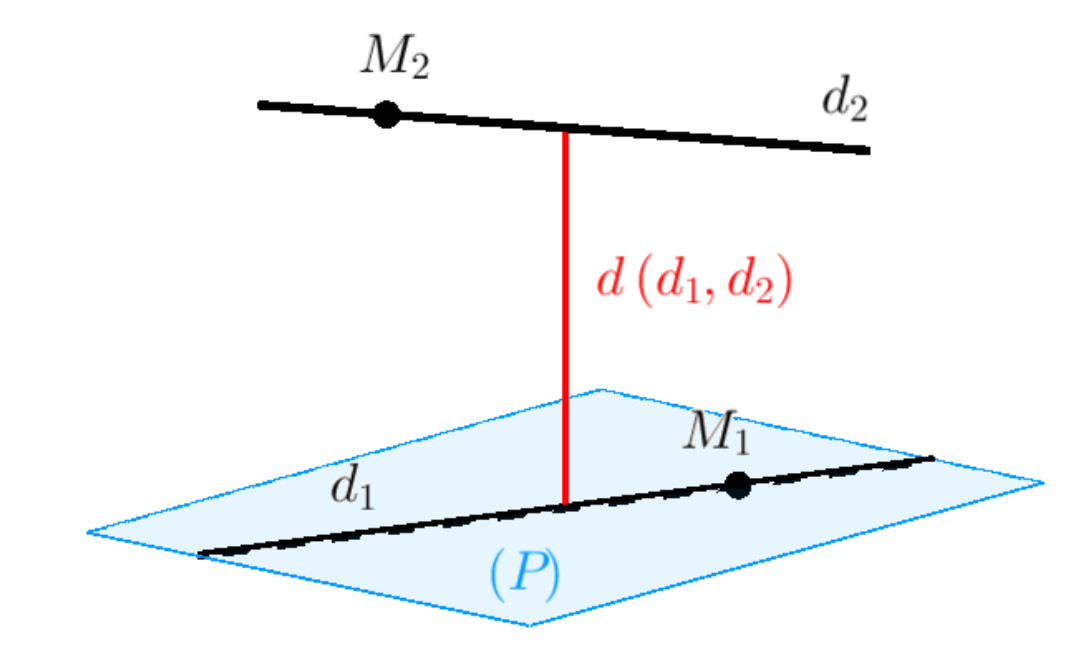
Hai đường thẳng được gọi là chéo nhau nếu chúng không đồng phẳng, tức là không cùng nằm trong một mặt phẳng. Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó. Đoạn vuông góc chung là đoạn thẳng nối hai điểm trên hai đường thẳng và vuông góc với cả hai đường thẳng.
Alt: Khoảng cách giữa hai đường thẳng chéo nhau được đo bằng độ dài đoạn vuông góc chung.
Lưu ý quan trọng: Đoạn vuông góc chung giữa hai đường thẳng chéo nhau là duy nhất.
2. Các Phương Pháp Tính Khoảng Cách Giữa Hai Đường Thẳng Chéo Nhau
Để tính khoảng cách 2 đường thẳng chéo nhau, bạn cần nắm vững các kiến thức về hình học không gian, đặc biệt là các phương pháp tính khoảng cách từ một điểm đến một mặt phẳng và cách dựng hình chiếu vuông góc. Dưới đây là 3 phương pháp phổ biến nhất:
2.1. Phương Pháp 1: Dựng và Tính Độ Dài Đoạn Vuông Góc Chung
Đây là phương pháp trực quan và thường được sử dụng khi hai đường thẳng chéo nhau và vuông góc với nhau.
Công thức tổng quát:
Nếu AB là đoạn vuông góc chung của hai đường thẳng a và b, thì:
AB ⊥ a
AB ⊥ b
AB cắt a
AB cắt b
=> d(a, b) = ABKhi hai đường thẳng a và b vừa chéo nhau, vừa vuông góc với nhau, thường tồn tại một mặt phẳng (α) chứa a và vuông góc với b. Các bước dựng đoạn vuông góc chung:
- Tìm giao điểm H của b và (α).
- Trong (α), dựng HK vuông góc với a tại K. HK là đoạn vuông góc chung của a và b. Tính độ dài HK để tìm khoảng cách 2 đường thẳng chéo nhau.
Alt: Hình ảnh minh họa cách dựng đoạn vuông góc chung để tính khoảng cách khi hai đường thẳng vuông góc.
Lưu ý: Phương pháp này hiệu quả nhất khi hai đường thẳng vuông góc với nhau. Nếu không, việc dựng đoạn vuông góc chung có thể rất phức tạp.
Ví dụ minh họa:
(Hình ảnh và ví dụ từ bài gốc, giữ nguyên để đảm bảo tính liên tục)
Alt: Ví dụ tính khoảng cách hai đường thẳng chéo nhau bằng cách dựng đường vuông góc chung.
Alt: Bài tập ví dụ về khoảng cách giữa hai đường thẳng chéo nhau, sử dụng phương pháp dựng đoạn vuông góc.
2.2. Phương Pháp 2: Tính Khoảng Cách Từ Đường Thẳng Đến Mặt Phẳng Song Song
Khi hai đường thẳng a và b chéo nhau nhưng không vuông góc, ta sử dụng phương pháp này. Ý tưởng chính là tìm một mặt phẳng chứa một đường thẳng và song song với đường thẳng còn lại, sau đó tính khoảng cách từ đường thẳng đến mặt phẳng đó.
Các bước thực hiện:
- Chọn mặt phẳng (α): Chọn (α) chứa đường thẳng b và song song với đường thẳng a.
- Dựng hình chiếu vuông góc d: Dựng đường thẳng d là hình chiếu vuông góc của a xuống (α). Lấy điểm M thuộc a, dựng MN vuông góc với (α). Đường thẳng d đi qua N và song song với a.
- Tìm đoạn vuông góc chung: Gọi H là giao điểm của d và b, dựng HK song song với MN. HK là đoạn vuông góc chung của a và b, và độ dài HK bằng MN.
Alt: Hình vẽ minh họa cách tính khoảng cách giữa hai đường thẳng chéo nhau bằng cách đưa về khoảng cách từ đường thẳng đến mặt phẳng song song.
Ví dụ minh họa:
(Ví dụ từ bài gốc, giữ nguyên)
Alt: Bài toán tính khoảng cách giữa hai đường thẳng chéo nhau SM và BC trong hình chóp.
Alt: Minh họa tính khoảng cách giữa hai đường thẳng chéo nhau AB và SC, áp dụng phương pháp mặt phẳng song song.
2.3. Phương Pháp 3: Tính Khoảng Cách Giữa Hai Mặt Phẳng Song Song
Phương pháp này chuyển việc tính khoảng cách 2 đường thẳng chéo nhau về việc tính khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.
Công thức:
a ⊂ (P)
b ⊂ (Q)
(P) // (Q)
=> d(a, b) = d((P), (Q))Lưu ý: Phương pháp này thường được sử dụng khi việc dựng đường thẳng song song với một trong hai đường thẳng ban đầu gặp khó khăn.
Ví dụ minh họa:
(Ví dụ từ bài gốc, giữ nguyên)
Alt: Ví dụ minh họa tính khoảng cách hai đường thẳng chéo nhau trong hình lập phương bằng cách sử dụng hai mặt phẳng song song.
Alt: Các bước giải chi tiết bài toán tính khoảng cách giữa hai đường thẳng chéo nhau trong hình lập phương.
Alt: Bài toán tính khoảng cách giữa hai đường thẳng chéo nhau MN và HP trong hình hộp chữ nhật.
Alt: Hướng dẫn giải chi tiết bài toán về khoảng cách giữa hai đường thẳng chéo nhau trong hình hộp đứng.
3. Bài Tập Về Khoảng Cách Hai Đường Thẳng Chéo Nhau (Có Lời Giải)
Để củng cố kiến thức, hãy cùng giải các bài tập sau:
(Các bài tập và lời giải từ bài gốc được giữ lại)
Bài 1:
Alt: Đề bài toán hình học không gian, yêu cầu tính khoảng cách giữa hai đường thẳng chéo nhau.
Giải:
Alt: Lời giải chi tiết cho bài toán khoảng cách hai đường thẳng chéo nhau, kèm hình vẽ minh họa.
Bài 2:
Alt: Bài tập tính khoảng cách giữa hai đường thẳng chéo nhau trong không gian.
Giải:
Alt: Hướng dẫn giải bài tập về khoảng cách hai đường thẳng chéo nhau, từng bước một.
(Các bài tập và lời giải còn lại được giữ nguyên tương tự…)
Bài 3:
Alt: Đề bài toán tìm khoảng cách giữa hai đường thẳng chéo nhau trong hình học.
Giải:
Alt: Các bước giải chi tiết bài toán khoảng cách giữa hai đường thẳng chéo nhau.
Bài 4:
Alt: Bài tập về tính khoảng cách hai đường thẳng chéo nhau trong hình chóp, có hình vẽ.
Giải:
Alt: Giải chi tiết bài toán khoảng cách giữa hai đường thẳng chéo nhau trong hình chóp.
Bài 5:
Alt: Đề bài tập tính khoảng cách hai đường thẳng chéo nhau, minh họa hình học.
Giải:
Alt: Chi tiết cách giải bài toán khoảng cách hai đường thẳng chéo nhau, có giải thích rõ ràng.
Bài 6:
Alt: Bài tập hình học về tính khoảng cách giữa hai đường thẳng chéo nhau.
Giải:
Alt: Hướng dẫn giải bài tập khoảng cách giữa hai đường thẳng chéo nhau, từng bước cụ thể.
Bài 7:
Alt: Đề bài toán hình học không gian, tính khoảng cách giữa hai đường thẳng chéo nhau.
Giải:
Alt: Cách giải chi tiết bài toán khoảng cách giữa hai đường thẳng chéo nhau.
Bài 8:
Alt: Bài tập về khoảng cách giữa hai đường thẳng chéo nhau trong hình chóp.
Giải:
Alt: Các bước giải bài tập khoảng cách hai đường thẳng chéo nhau một cách dễ hiểu.
Bài 9:
Alt: Đề bài toán về khoảng cách giữa hai đường thẳng chéo nhau, có hình vẽ minh họa.
Giải:
Alt: Giải thích các bước giải bài toán khoảng cách hai đường thẳng chéo nhau.
Bài 10:
Alt: Bài tập cuối cùng về khoảng cách giữa hai đường thẳng chéo nhau.
Giải:
Alt: Hướng dẫn giải bài tập cuối cùng về khoảng cách giữa hai đường thẳng chéo nhau.
Hy vọng với những kiến thức và bài tập trên, bạn sẽ nắm vững cách tính khoảng cách 2 đường thẳng chéo nhau và tự tin giải quyết các bài toán liên quan. Chúc bạn thành công!