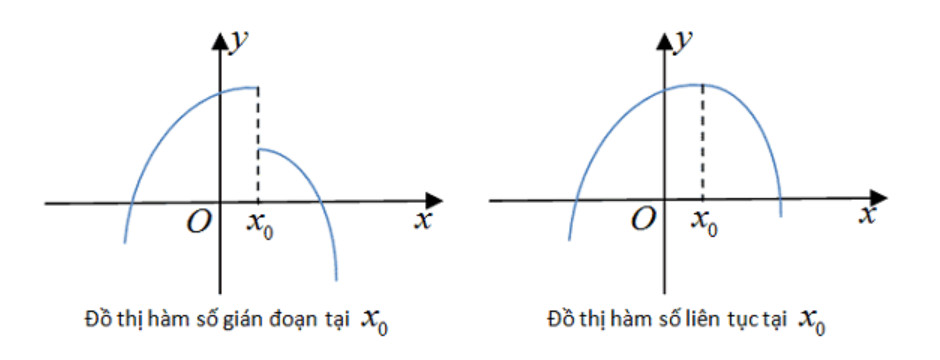Khi Nào Hàm Số Liên Tục Trên R?

Hàm số liên tục là một khái niệm quan trọng trong giải tích toán học. Việc xác định khi nào một hàm số liên tục trên tập số thực R có nhiều ứng dụng trong giải toán và các lĩnh vực khoa học khác. Bài viết này sẽ trình bày chi tiết về điều kiện, định lý và các dạng bài tập liên quan đến hàm số liên tục trên R.

1. Định Nghĩa Hàm Số Liên Tục

Một hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm thuộc khoảng đó. Điều này có nghĩa là, tại mỗi điểm x₀ trong khoảng, giới hạn của f(x) khi x tiến đến x₀ phải bằng giá trị của hàm số tại điểm đó, tức là:

lim (x→x₀) f(x) = f(x₀)

Nếu hàm số không thỏa mãn điều kiện này tại một điểm, ta nói rằng hàm số gián đoạn tại điểm đó.

Đồ thị hàm số liên tục, thể hiện sự liền mạch của đồ thị trên một khoảng xác định, không có điểm gián đoạn.

2. Điều Kiện Để Hàm Số Liên Tục Trên R

Hàm số y = f(x) được gọi là liên tục trên R nếu nó liên tục tại mọi điểm x thuộc R. Để chứng minh một hàm số liên tục trên R, ta cần kiểm tra tính liên tục tại mọi điểm. Tuy nhiên, có một số loại hàm số mà ta có thể kết luận ngay tính liên tục trên R mà không cần chứng minh chi tiết:

• Hàm đa thức: Các hàm số có dạng P(x) = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + … + a₁x + a₀, với aᵢ là các hằng số, luôn liên tục trên R.
• Hàm lượng giác: Các hàm số y = sin(x) và y = cos(x) liên tục trên R.
• Hàm mũ: Các hàm số y = aˣ (với a > 0) liên tục trên R.

Đối với các hàm số phức tạp hơn, ta cần xét tính liên tục tại các điểm đặc biệt, thường là các điểm mà biểu thức của hàm số thay đổi hoặc không xác định.

3. Các Định Lý Về Hàm Số Liên Tục

Có một số định lý quan trọng liên quan đến hàm số liên tục giúp chúng ta dễ dàng xác định tính liên tục của các hàm số phức tạp:

• Định lý 1: Tổng, hiệu và tích của hai hàm số liên tục tại một điểm cũng là một hàm số liên tục tại điểm đó. Thương của hai hàm số liên tục tại một điểm cũng liên tục tại điểm đó, miễn là mẫu số khác không.
• Định lý 2: Nếu hàm số y = f(x) liên tục trên đoạn [a, b] và f(a) * f(b) < 0, thì tồn tại ít nhất một điểm c thuộc khoảng (a, b) sao cho f(c) = 0. Đây là định lý về giá trị trung gian, thường được sử dụng để chứng minh sự tồn tại nghiệm của phương trình.

4. Các Dạng Bài Tập Thường Gặp

4.1. Xét Tính Liên Tục Của Hàm Số Tại Một Điểm

Để xét tính liên tục của hàm số y = f(x) tại điểm x₀, ta thực hiện các bước sau:

1. Tính f(x₀).
2. Tính lim (x→x₀) f(x).
3. So sánh hai giá trị trên. Nếu lim (x→x₀) f(x) = f(x₀), thì hàm số liên tục tại x₀. Ngược lại, hàm số gián đoạn tại x₀.

Ví dụ: Xét tính liên tục của hàm số sau tại x = 1:

f(x) = { (x² – 1) / (x – 1) khi x ≠ 1
{ 2 khi x = 1

Giải:

1. f(1) = 2.
2. lim (x→1) f(x) = lim (x→1) (x² – 1) / (x – 1) = lim (x→1) (x + 1) = 2.
3. Vì lim (x→1) f(x) = f(1) = 2, hàm số liên tục tại x = 1.

4.2. Tìm Điều Kiện Để Hàm Số Liên Tục

Dạng bài tập này yêu cầu tìm giá trị của một tham số (thường là m) để hàm số liên tục tại một điểm hoặc trên một khoảng. Ta thực hiện các bước tương tự như trên, nhưng cần giải phương trình hoặc bất phương trình để tìm giá trị của tham số.

Ví dụ: Tìm m để hàm số sau liên tục tại x = 0:

f(x) = { (sin(mx)) / x khi x ≠ 0
{ 1 khi x = 0

Giải:

1. f(0) = 1.
2. lim (x→0) f(x) = lim (x→0) (sin(mx)) / x = m (áp dụng quy tắc L’Hopital hoặc giới hạn cơ bản lim (x→0) sin(x) / x = 1).
3. Để hàm số liên tục tại x = 0, ta cần lim (x→0) f(x) = f(0), tức là m = 1.

4.3. Chứng Minh Phương Trình Có Nghiệm

Sử dụng định lý giá trị trung gian để chứng minh phương trình f(x) = 0 có nghiệm trên một khoảng (a, b). Ta cần chứng minh f(x) liên tục trên [a, b] và f(a) * f(b) < 0.

Ví dụ: Chứng minh phương trình x³ + x – 1 = 0 có nghiệm trên khoảng (0, 1).

Giải:

1. f(x) = x³ + x – 1 là hàm đa thức, nên liên tục trên R, do đó liên tục trên [0, 1].
2. f(0) = -1 và f(1) = 1.
3. f(0) f(1) = -1 1 = -1 < 0.
4. Theo định lý giá trị trung gian, tồn tại ít nhất một điểm c thuộc (0, 1) sao cho f(c) = 0. Vậy phương trình có nghiệm trên khoảng (0, 1).

Ví dụ minh họa hàm số liên tục trên một đoạn, thể hiện f(a) và f(b) trái dấu, chứng minh sự tồn tại ít nhất một nghiệm trên khoảng (a, b).

5. Kết Luận

Việc nắm vững khái niệm và các định lý về hàm số liên tục là rất quan trọng trong chương trình toán học phổ thông và cao cấp. Hiểu rõ điều kiện để một hàm số liên tục trên R, cùng với các dạng bài tập thường gặp, sẽ giúp học sinh và sinh viên giải quyết các bài toán liên quan một cách hiệu quả. Hy vọng bài viết này đã cung cấp đầy đủ kiến thức cần thiết để bạn đọc tự tin chinh phục các bài toán về hàm số liên tục.