Đường tròn là một hình học cơ bản và quen thuộc. Một trong những đặc điểm thú vị của nó là tính đối xứng. Vậy, “Hình Tròn Có Bao Nhiêu Trục đối Xứng?” và các trục đối xứng này được xác định như thế nào? Chúng ta sẽ cùng tìm hiểu chi tiết trong bài viết này.
Định nghĩa trục đối xứng: Trục đối xứng của một hình là đường thẳng mà khi ta gấp hình đó theo đường thẳng này, hai nửa của hình sẽ trùng khít lên nhau.
Vậy hình tròn có bao nhiêu trục đối xứng? Câu trả lời là hình tròn có vô số trục đối xứng.
Trục đối xứng của hình tròn là bất kỳ đường thẳng nào đi qua tâm của đường tròn đó. Vì có vô số đường thẳng có thể đi qua tâm của đường tròn, nên hình tròn có vô số trục đối xứng. Mỗi đường kính của hình tròn chính là một trục đối xứng.
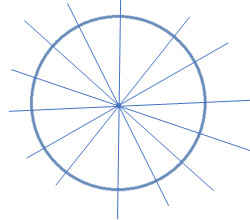Minh họa vô số trục đối xứng của hình tròn đi qua tâm O
Lý do hình tròn có vô số trục đối xứng:
Tính đối xứng của hình tròn xuất phát từ định nghĩa của nó: Tập hợp tất cả các điểm cách đều một điểm cố định (tâm). Do đó, bất kỳ đường thẳng nào đi qua tâm cũng chia hình tròn thành hai phần hoàn toàn giống nhau.
Hình ảnh minh họa một đường thẳng đi qua tâm hình tròn, chia nó thành hai nửa đối xứng hoàn hảo. Bất kỳ đường thẳng nào khác đi qua tâm cũng sẽ tạo ra một phép chia tương tự. Đây là lý do tại sao hình tròn có vô số trục đối xứng, làm cho nó trở thành một hình học đặc biệt và quan trọng trong toán học và ứng dụng thực tế.
Ứng dụng của tính đối xứng của hình tròn:
Tính đối xứng của hình tròn không chỉ là một khái niệm toán học thuần túy mà còn có nhiều ứng dụng thực tế trong cuộc sống hàng ngày, kỹ thuật, và nghệ thuật. Ví dụ:
- Trong kỹ thuật: Bánh xe, ổ bi, và nhiều bộ phận máy móc khác được thiết kế dựa trên hình tròn để đảm bảo sự cân bằng và hoạt động trơn tru.
- Trong kiến trúc: Các mái vòm, cửa sổ tròn, và các yếu tố trang trí hình tròn được sử dụng để tạo ra sự hài hòa và cân đối cho công trình.
- Trong nghệ thuật: Hình tròn được sử dụng rộng rãi trong thiết kế đồ họa, trang trí, và các tác phẩm nghệ thuật khác để tạo ra sự cân bằng và thu hút thị giác.
Hiểu rõ về trục đối xứng của hình tròn giúp chúng ta không chỉ nắm vững kiến thức toán học mà còn đánh giá cao vẻ đẹp và tính ứng dụng của nó trong thế giới xung quanh.
