Hình thoi là một dạng tứ giác đặc biệt, thu hút sự quan tâm không chỉ trong lĩnh vực toán học mà còn trong nhiều ứng dụng thực tế. Bài viết này sẽ đi sâu vào các khía cạnh liên quan đến “Hình Thoi Cạnh A”, từ định nghĩa, tính chất, công thức tính toán đến các bài toán ứng dụng.
Định Nghĩa và Tính Chất Cơ Bản của Hình Thoi
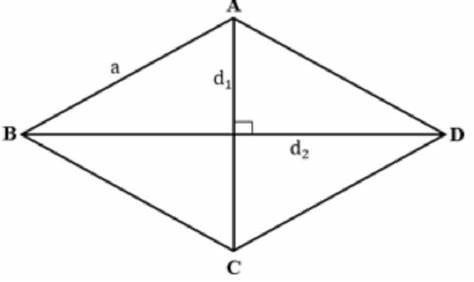
Hình thoi là một tứ giác có bốn cạnh bằng nhau. Đây là đặc điểm nổi bật nhất và là tiền đề cho nhiều tính chất thú vị khác.
- Tính chất:
- Các cạnh đối song song.
- Hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường.
- Hai đường chéo là các đường phân giác của các góc trong hình thoi.
- Là hình bình hành có hai cạnh kề bằng nhau.
Đường Chéo của Hình Thoi: Vai Trò và Tính Chất
Đường chéo của hình thoi đóng vai trò quan trọng trong việc xác định các tính chất và tính toán liên quan đến hình này. Chúng là đoạn thẳng nối hai đỉnh đối diện.
- Tính chất quan trọng:
- Hai đường chéo không nhất thiết bằng nhau (trừ khi hình thoi là hình vuông).
- Hai đường chéo cắt nhau tại trung điểm và vuông góc với nhau. Điều này tạo ra bốn tam giác vuông bằng nhau bên trong hình thoi.
- Mỗi đường chéo chia hình thoi thành hai tam giác cân bằng nhau.
Công Thức Tính Đường Chéo Hình Thoi Cạnh a
Khi biết cạnh của hình thoi (a) và một số thông tin khác, ta có thể tính được độ dài đường chéo. Dưới đây là một số công thức phổ biến:
-
Khi biết diện tích (S) và một đường chéo (d1):
Đường chéo còn lại (d2) được tính bằng công thức:
d2 = (2 * S) / d1 -
Khi biết cạnh (a) và một góc (α):
Giả sử góc α là góc tạo bởi hai cạnh kề nhau. Đường chéo ngắn (d1) và đường chéo dài (d2) có thể được tính như sau:
d1 = 2 * a * sin(α/2)d2 = 2 * a * cos(α/2)
-
Sử dụng Định lý Pytago:
Vì hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm, ta có thể áp dụng định lý Pytago trong tam giác vuông tạo bởi nửa độ dài hai đường chéo và cạnh hình thoi:
(d1/2)^2 + (d2/2)^2 = a^2
Từ đó, nếu biết một đường chéo và cạnh, ta có thể suy ra đường chéo còn lại.
Ví dụ: Cho hình thoi ABCD có cạnh a và góc ABC = 60 độ. Tính độ dài đường chéo AC.
Giải: Vì ABCD là hình thoi nên AB = BC = a. Tam giác ABC có AB = BC = a và góc ABC = 60 độ, suy ra tam giác ABC là tam giác đều cạnh a. Vậy, AC = a.
Bài Tập Vận Dụng về Hình Thoi Cạnh a
Dưới đây là một số bài toán ví dụ để minh họa cách áp dụng các công thức và tính chất của hình thoi cạnh a.
Bài toán 1: Một hình thoi có diện tích 360 cm² và một đường chéo dài 24 cm. Tính độ dài đường chéo còn lại.
Giải: Áp dụng công thức d2 = (2 * S) / d1, ta có: d2 = (2 * 360) / 24 = 30 cm.
Bài toán 2: Cho hình thoi ABCD có hai đường chéo dài 160 cm và 120 cm. Tính chiều cao của hình thoi, biết tỉ số giữa chiều cao và cạnh là 24:25.
Giải:
- Diện tích hình thoi: S = (160 * 120) / 2 = 9600 cm².
- Gọi chiều cao là 24x, cạnh là 25x. Khi đó, diện tích hình thoi cũng có thể tính bằng: S = 24x * 25x = 600x².
- Suy ra, 600x² = 9600 => x² = 16 => x = 4.
- Chiều cao hình thoi: h = 24 * 4 = 96 cm.
Ứng Dụng Thực Tế của Hình Thoi
Hình thoi không chỉ là một khái niệm toán học trừu tượng, mà còn xuất hiện trong nhiều lĩnh vực của đời sống, bao gồm:
- Kiến trúc: Các họa tiết hình thoi thường được sử dụng trong trang trí mặt tiền, lát sàn, hoặc thiết kế cửa sổ.
- Thiết kế: Hình thoi là một hình dạng phổ biến trong thiết kế đồ họa, logo, và các sản phẩm trang trí.
- Kỹ thuật: Các cấu trúc hình thoi có độ bền cao và khả năng chịu lực tốt, được ứng dụng trong xây dựng cầu đường và các công trình kỹ thuật khác.
- Nghệ thuật: Hình thoi xuất hiện trong nhiều tác phẩm nghệ thuật truyền thống và hiện đại.
Hiểu rõ về “hình thoi cạnh a” không chỉ giúp chúng ta giải quyết các bài toán hình học mà còn mở ra những ứng dụng sáng tạo trong thực tế. Hy vọng bài viết này đã cung cấp cho bạn cái nhìn toàn diện và sâu sắc về hình thoi.