Trong hình học, việc xác định một hình có nội tiếp được đường tròn hay không là một bài toán quan trọng. Một tứ giác được gọi là nội tiếp đường tròn nếu có một đường tròn đi qua tất cả các đỉnh của tứ giác đó. Vậy những hình nào có tính chất đặc biệt này? Chúng ta sẽ cùng tìm hiểu chi tiết.
1. Hình Chữ Nhật
Hình chữ nhật là một tứ giác có bốn góc vuông. Một hình chữ nhật luôn nội tiếp được trong một đường tròn. Tâm của đường tròn này là giao điểm của hai đường chéo, và bán kính của đường tròn bằng nửa độ dài đường chéo.
Alt text: Hình chữ nhật ABCD nội tiếp đường tròn tâm O, đường kính AC minh họa tính chất hình chữ nhật nội tiếp được đường tròn.
Để chứng minh, ta có thể sử dụng tính chất tổng hai góc đối của tứ giác nội tiếp bằng 180 độ. Trong hình chữ nhật, mỗi góc bằng 90 độ, do đó tổng hai góc đối diện luôn bằng 180 độ, suy ra hình chữ nhật nội tiếp được đường tròn.
2. Hình Vuông
Hình vuông là một trường hợp đặc biệt của hình chữ nhật, nó vừa là hình chữ nhật vừa là hình thoi. Vì hình vuông là hình chữ nhật nên nó cũng nội tiếp được trong một đường tròn. Tâm đường tròn ngoại tiếp hình vuông là giao điểm của hai đường chéo, và bán kính bằng nửa độ dài đường chéo.
Alt text: Hình vuông ABCD nội tiếp đường tròn với tâm là giao điểm hai đường chéo, ví dụ trực quan về hình vuông nội tiếp đường tròn.
3. Hình Thang Cân
Hình thang cân là hình thang có hai cạnh bên bằng nhau. Một hình thang cân cũng nội tiếp được trong một đường tròn.
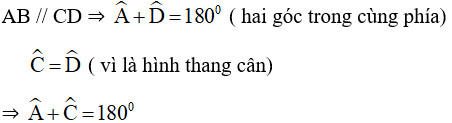Hình thang cân ABCD nội tiếp đường tròn
Alt text: Minh họa hình thang cân ABCD nội tiếp đường tròn, cạnh AB song song CD, AD = BC.
Để chứng minh hình thang cân nội tiếp được đường tròn, ta cần chứng minh tổng hai góc đối bằng 180 độ. Gọi ABCD là hình thang cân (AB // CD và AD = BC). Khi đó, góc A + góc C = 180 độ (do cùng bù với góc D), và góc B + góc D = 180 độ (do cùng bù với góc C).
4. Các Hình Không Nội Tiếp Được Đường Tròn
- Hình bình hành: Nói chung, hình bình hành không nội tiếp được đường tròn, trừ trường hợp nó là hình chữ nhật hoặc hình vuông.
- Hình thang vuông: Hình thang vuông (hình thang có một góc vuông) không nội tiếp được đường tròn, trừ khi nó đồng thời là hình chữ nhật hoặc hình vuông.
Tổng Quát
Để một tứ giác nội tiếp được đường tròn, điều kiện cần và đủ là tổng hai góc đối diện của tứ giác bằng 180 độ. Việc nắm vững điều kiện này giúp ta dễ dàng xác định và chứng minh một hình có nội tiếp được đường tròn hay không.
