Trong hình học, một câu hỏi thường gặp là liệu một hình tứ giác có thể nội tiếp được trong một đường tròn hay không. Điều này có nghĩa là tất cả các đỉnh của tứ giác đó phải nằm trên đường tròn. Không phải hình tứ giác nào cũng thỏa mãn điều kiện này. Chúng ta sẽ cùng tìm hiểu về các loại hình và điều kiện để một hình có thể nội tiếp được đường tròn.
Điều kiện để một tứ giác nội tiếp được đường tròn
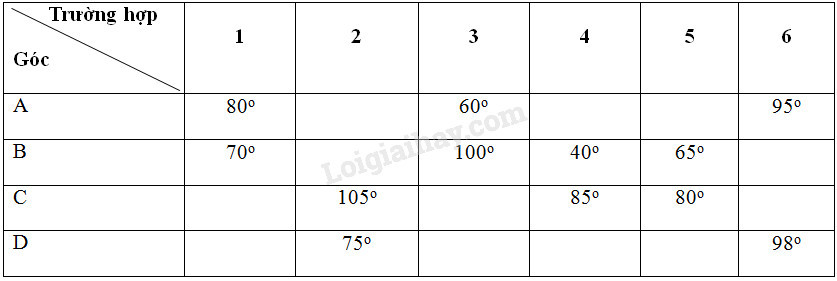
Một tứ giác được gọi là nội tiếp được trong một đường tròn khi và chỉ khi tổng hai góc đối diện của nó bằng 180 độ. Đây là một định lý quan trọng trong hình học và là cơ sở để xác định một tứ giác có nội tiếp được hay không.
Các hình tứ giác đặc biệt và khả năng nội tiếp
-
Hình bình hành: Hình bình hành có các góc đối bằng nhau, nhưng tổng hai góc đối thường không bằng 180 độ, trừ khi nó là hình chữ nhật hoặc hình vuông. Do đó, hình bình hành nói chung không nội tiếp được đường tròn.
-
Hình chữ nhật: Hình chữ nhật có bốn góc vuông, tức là mỗi góc bằng 90 độ. Tổng hai góc đối của hình chữ nhật luôn bằng 180 độ (90 + 90 = 180). Vì vậy, hình chữ nhật luôn nội tiếp được đường tròn.
-
Hình vuông: Tương tự như hình chữ nhật, hình vuông cũng có bốn góc vuông. Do đó, hình vuông luôn nội tiếp được đường tròn.
-
Hình thang: Hình thang là tứ giác có ít nhất một cặp cạnh đối song song. Hình thang nói chung không nội tiếp được đường tròn.
-
Hình thang vuông: Hình thang vuông là hình thang có ít nhất một góc vuông. Hình thang vuông nói chung không nội tiếp được đường tròn.
-
Hình thang cân: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. Hình thang cân luôn nội tiếp được đường tròn. Lý do là vì các góc ở đáy bằng nhau và tổng các góc trong một tứ giác là 360 độ, nên tổng hai góc đối sẽ bằng 180 độ.
Ví dụ cụ thể
Để hiểu rõ hơn, chúng ta xét một số ví dụ. Giả sử ta có một hình bình hành ABCD. Nếu góc A không bằng 90 độ, thì tổng góc A và góc C (góc đối của A) sẽ không bằng 180 độ. Do đó, hình bình hành này không thể nội tiếp được đường tròn.
Ngược lại, nếu ta có một hình thang cân ABCD (AB song song CD, góc A = góc B), thì góc A + góc C = 180 độ, và góc B + góc D = 180 độ. Do đó, hình thang cân này có thể nội tiếp được đường tròn.
Kết luận
Tóm lại, không phải hình tứ giác nào cũng nội tiếp được đường tròn. Điều kiện cần và đủ để một tứ giác nội tiếp được đường tròn là tổng hai góc đối của nó phải bằng 180 độ. Dựa vào điều kiện này, chúng ta có thể xác định được hình chữ nhật, hình vuông và hình thang cân là những hình luôn nội tiếp được đường tròn, trong khi hình bình hành, hình thang và hình thang vuông nói chung là không.