Trong thế giới hình học, tứ giác là một hình dạng quen thuộc với nhiều ứng dụng thực tế. Bên cạnh những tính chất chung, một số loại tứ giác sở hữu những đặc điểm riêng biệt, trong đó có đặc điểm về độ dài đường chéo. Vậy, Hình Nào Có Hai đường Chéo Bằng Nhau? Chúng ta hãy cùng khám phá!
Tính Chất Chung Của Tứ Giác
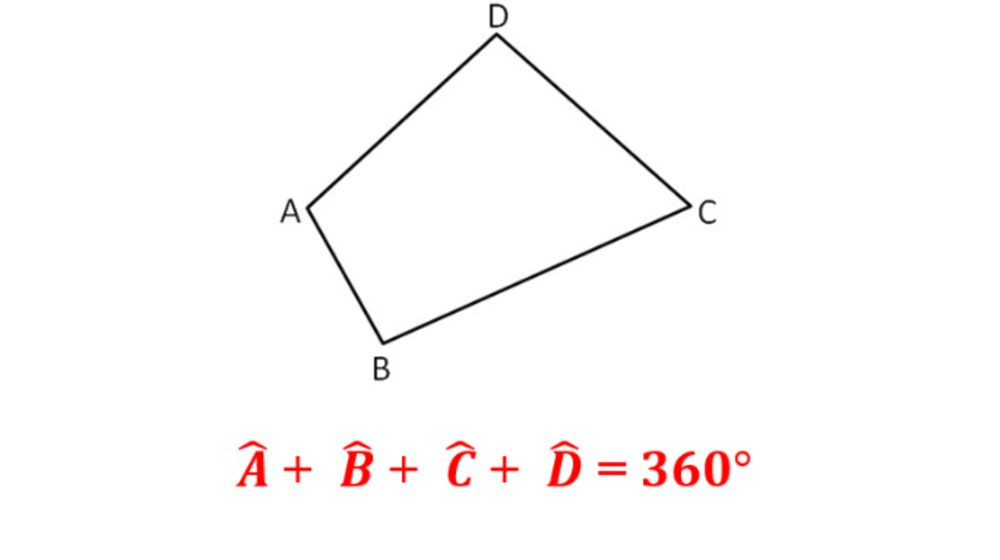
Trước khi đi sâu vào các loại tứ giác đặc biệt, hãy cùng ôn lại những kiến thức cơ bản về tứ giác:
- Định nghĩa: Tứ giác là một đa giác có bốn đỉnh và bốn cạnh.
- Tổng góc: Tổng các góc trong một tứ giác luôn bằng 360 độ.
Các Loại Tứ Giác Có Hai Đường Chéo Bằng Nhau
Không phải tứ giác nào cũng có hai đường chéo bằng nhau. Đặc điểm này chỉ xuất hiện ở một số loại tứ giác đặc biệt, bao gồm:
1. Hình Chữ Nhật
Hình chữ nhật là một tứ giác có bốn góc vuông. Một tính chất quan trọng của hình chữ nhật là hai đường chéo của nó bằng nhau và cắt nhau tại trung điểm của mỗi đường.
2. Hình Vuông
Hình vuông là một trường hợp đặc biệt của hình chữ nhật, đồng thời cũng là một hình thoi. Nó có bốn góc vuông và bốn cạnh bằng nhau. Giống như hình chữ nhật, hai đường chéo của hình vuông cũng bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
3. Hình Thang Cân
Hình thang cân là một hình thang (tứ giác có ít nhất một cặp cạnh đối song song) có hai góc kề một đáy bằng nhau. Một tính chất quan trọng của hình thang cân là hai đường chéo của nó bằng nhau.
Phân Biệt Các Loại Tứ Giác
Để tránh nhầm lẫn, cần phân biệt rõ đặc điểm của từng loại tứ giác:
- Hình bình hành: Có các cạnh đối song song và bằng nhau, các góc đối bằng nhau, nhưng đường chéo không nhất thiết bằng nhau.
- Hình thoi: Có bốn cạnh bằng nhau, nhưng đường chéo không nhất thiết bằng nhau (chỉ bằng nhau khi là hình vuông).
Ứng Dụng Thực Tế
Việc nhận biết các loại tứ giác và tính chất của chúng có nhiều ứng dụng trong thực tế, từ xây dựng, thiết kế đến các bài toán hình học. Ví dụ, việc sử dụng hình chữ nhật và hình vuông trong xây dựng giúp đảm bảo tính vuông góc và cân đối của công trình.
Kết Luận
Như vậy, các hình có hai đường chéo bằng nhau bao gồm hình chữ nhật, hình vuông và hình thang cân. Việc nắm vững kiến thức về các loại tứ giác và tính chất của chúng sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và hiệu quả hơn. Hãy luyện tập thường xuyên để ghi nhớ và áp dụng kiến thức này vào thực tế!