Hình Lăng Trụ Tứ Giác đều là một dạng hình học không gian đặc biệt, thường gặp trong các bài toán hình học và ứng dụng thực tế. Bài viết này sẽ cung cấp một cái nhìn toàn diện về hình lăng trụ tứ giác đều, bao gồm định nghĩa, các tính chất quan trọng, công thức tính toán và một số ứng dụng tiêu biểu.
Định nghĩa hình lăng trụ tứ giác đều
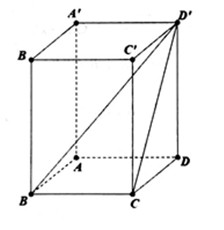
Hình lăng trụ tứ giác đều là một hình lăng trụ đứng có đáy là hình vuông. Điều này có nghĩa là:
- Hai đáy là hai hình vuông bằng nhau và song song với nhau.
- Các mặt bên là các hình chữ nhật bằng nhau và vuông góc với hai mặt đáy.
Các tính chất quan trọng của hình lăng trụ tứ giác đều
- Tính đối xứng: Hình lăng trụ tứ giác đều có tính đối xứng cao. Nó có trục đối xứng là đường thẳng đi qua tâm của hai đáy và có mặt phẳng đối xứng là mặt phẳng trung trực của các cạnh bên.
- Các đường chéo: Các đường chéo của các mặt bên bằng nhau.
- Các mặt: Có hai mặt đáy là hình vuông và bốn mặt bên là hình chữ nhật.
- Các cạnh: Có 8 đỉnh, 12 cạnh (4 cạnh đáy trên, 4 cạnh đáy dưới và 4 cạnh bên).
Công thức tính toán liên quan đến hình lăng trụ tứ giác đều
Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy là a và chiều cao là h.
-
Diện tích đáy (Sđáy):
Sđáy = a² -
Diện tích xung quanh (Sxq):
Sxq = 4ah(vì có 4 mặt bên là hình chữ nhật bằng nhau) -
Diện tích toàn phần (Stp):
Stp = Sxq + 2Sđáy = 4ah + 2a² -
Thể tích (V):
V = Sđáy * h = a²h
Ví dụ minh họa
Xét một hình lăng trụ tứ giác đều có cạnh đáy a = 4cm và chiều cao h = 6cm. Ta có:
- Diện tích đáy:
Sđáy = 4² = 16 cm² - Diện tích xung quanh:
Sxq = 4 * 4 * 6 = 96 cm² - Diện tích toàn phần:
Stp = 96 + 2 * 16 = 128 cm² - Thể tích:
V = 16 * 6 = 96 cm³
Ứng dụng của hình lăng trụ tứ giác đều
Hình lăng trụ tứ giác đều xuất hiện nhiều trong thực tế, ví dụ như:
- Kiến trúc: Các tòa nhà, cột trụ, hoặc các khối trang trí có dạng hình lăng trụ tứ giác đều.
- Đóng gói: Nhiều sản phẩm được đóng gói trong các hộp có dạng hình lăng trụ tứ giác đều để tối ưu hóa không gian và dễ dàng vận chuyển.
- Toán học và giáo dục: Dùng làm mô hình trực quan trong giảng dạy hình học không gian, giúp học sinh dễ dàng hình dung và nắm bắt các khái niệm.
Hình lăng trụ tứ giác đều là một hình học quan trọng với nhiều ứng dụng trong thực tế. Việc hiểu rõ định nghĩa, tính chất và công thức tính toán liên quan đến hình lăng trụ tứ giác đều giúp chúng ta giải quyết các bài toán hình học và ứng dụng chúng vào cuộc sống một cách hiệu quả.