Hình Chóp Tứ Giác đều Sabcd là một hình học không gian quan trọng, xuất hiện nhiều trong các bài toán và ứng dụng thực tế. Bài viết này sẽ cung cấp đầy đủ kiến thức về hình chóp tứ giác đều, từ định nghĩa, tính chất đến công thức tính toán và các bài tập vận dụng.
1. Khái Niệm Hình Chóp Tứ Giác Đều SABCD
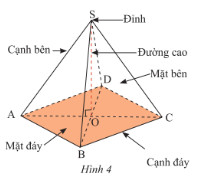
Hình chóp tứ giác đều SABCD là hình chóp có đáy là hình vuông và các mặt bên là những tam giác cân bằng nhau, có chung đỉnh.
Đặc điểm nhận dạng hình chóp tứ giác đều SABCD:
- Đáy ABCD là hình vuông.
- Các cạnh bên SA = SB = SC = SD.
- Các mặt bên (SAB, SBC, SCD, SDA) là các tam giác cân bằng nhau.
- Chân đường cao SO (O là giao điểm của AC và BD) trùng với tâm của hình vuông đáy ABCD.
- Các cạnh đáy AB = BC = CD = DA, là bốn cạnh của hình vuông đáy.
2. Các Yếu Tố Của Hình Chóp Tứ Giác Đều SABCD
- Đỉnh: S (đỉnh của hình chóp)
- Đáy: Hình vuông ABCD
- Cạnh bên: SA, SB, SC, SD
- Cạnh đáy: AB, BC, CD, DA
- Mặt bên: Các tam giác cân SAB, SBC, SCD, SDA
- Đường cao: SO (đường thẳng vuông góc với mặt đáy từ đỉnh S)
- Trung đoạn: Đường cao của mặt bên, xuất phát từ đỉnh S (ví dụ: SI trong tam giác SAB, với I là trung điểm AB)
3. Công Thức Tính Diện Tích và Thể Tích Hình Chóp Tứ Giác Đều SABCD
a. Diện Tích Xung Quanh
Diện tích xung quanh của hình chóp tứ giác đều SABCD bằng tổng diện tích của bốn mặt bên. Vì các mặt bên là các tam giác cân bằng nhau, ta có công thức:
Sxq = p * d
Trong đó:
Sxqlà diện tích xung quanh.plà nửa chu vi đáy (nửa chu vi hình vuông ABCD).dlà độ dài trung đoạn (chiều cao của một mặt bên).
b. Diện Tích Toàn Phần
Diện tích toàn phần của hình chóp tứ giác đều SABCD bằng tổng của diện tích xung quanh và diện tích đáy:
Stp = Sxq + Sđáy
Trong đó:
Stplà diện tích toàn phần.Sxqlà diện tích xung quanh.Sđáylà diện tích đáy (diện tích hình vuông ABCD).
c. Thể Tích
Thể tích của hình chóp tứ giác đều SABCD được tính bằng công thức:
V = (1/3) * Sđáy * h
Trong đó:
Vlà thể tích.Sđáylà diện tích đáy (diện tích hình vuông ABCD).hlà chiều cao của hình chóp (độ dài đoạn SO).
Ví dụ:
Cho hình chóp tứ giác đều SABCD có diện tích đáy là 16 cm² và chiều cao là 6 cm. Thể tích của hình chóp là:
V = (1/3) * 16 * 6 = 32 cm³
4. Bài Tập Vận Dụng
Bài 1: Tính diện tích xung quanh của hình chóp tứ giác đều SABCD, biết cạnh đáy AB = 5cm và trung đoạn SI = 8cm.
Giải:
- Nửa chu vi đáy: p = (4 * 5) / 2 = 10 cm
- Diện tích xung quanh: Sxq = p d = 10 8 = 80 cm²
Bài 2: Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng 6cm, chiều cao của hình chóp là 10cm. Tính thể tích của hình chóp đó.
Giải:
- Diện tích đáy: Sđáy = 6 * 6 = 36 cm²
- Thể tích: V = (1/3) 36 10 = 120 cm³
Bài 3: Một hình chóp tứ giác đều SABCD có thể tích bằng 100 cm³, chiều cao hình chóp bằng 12cm. Tính diện tích đáy của hình chóp đó.
Giải:
- Sđáy = (3 V) / h = (3 100) / 12 = 25 cm²
5. Ứng Dụng Thực Tế
Hình chóp tứ giác đều SABCD không chỉ là một khái niệm toán học mà còn xuất hiện trong nhiều ứng dụng thực tế, ví dụ như:
- Kiến trúc: Mái nhà, chóp tháp, các công trình có hình dạng tương tự.
- Thiết kế: Bao bì sản phẩm, đồ trang trí.
- Hình học: Giải các bài toán liên quan đến tính diện tích, thể tích trong không gian.
Hiểu rõ về hình chóp tứ giác đều SABCD, các công thức liên quan sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và áp dụng vào thực tiễn hiệu quả.