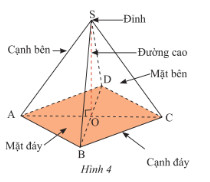
I. Khái Niệm Hình Chóp Tứ Giác Đều
Hình Chóp Tứ Giác đều là một hình không gian đặc biệt, có những tính chất hình học quan trọng và được ứng dụng nhiều trong thực tế. Để hiểu rõ hơn về hình chóp tứ giác đều, ta cần nắm vững các yếu tố cấu thành và đặc điểm của nó.
Một hình chóp được gọi là hình chóp tứ giác đều nếu nó thỏa mãn các điều kiện sau:
- Đáy là hình vuông: Mặt đáy của hình chóp là một hình vuông. Đây là yếu tố quan trọng để phân biệt với các loại hình chóp tứ giác khác.
- Các cạnh bên bằng nhau: Bốn cạnh bên của hình chóp có độ dài bằng nhau. Điều này đảm bảo tính đối xứng của hình chóp.
- Các mặt bên là các tam giác cân bằng nhau và có chung một đỉnh: Bốn mặt bên của hình chóp là các tam giác cân, chúng có diện tích bằng nhau và cùng chung một đỉnh (đỉnh của hình chóp).
- Chân đường cao trùng với giao điểm của hai đường chéo của mặt đáy: Đường cao của hình chóp (đường thẳng vuông góc với mặt đáy và đi qua đỉnh) có chân trùng với giao điểm của hai đường chéo của hình vuông đáy. Điểm này cũng là tâm đối xứng của hình vuông đáy.
Alt text: Mô tả hình chóp tứ giác đều với đáy hình vuông ABCD, đỉnh S, các cạnh bên SA, SB, SC, SD bằng nhau và đường cao SO vuông góc với đáy tại O (giao điểm hai đường chéo AC và BD).
II. Công Thức Tính Diện Tích Xung Quanh và Thể Tích
1. Diện Tích Xung Quanh
Diện tích xung quanh của hình chóp tứ giác đều là tổng diện tích của bốn mặt bên. Do các mặt bên là các tam giác cân bằng nhau, ta có thể tính diện tích xung quanh bằng công thức:
Sxq = p * d
Trong đó:
Sxqlà diện tích xung quanh của hình chóp.plà nửa chu vi đáy (nửa chu vi của hình vuông đáy).dlà trung đoạn của hình chóp (chiều cao của một mặt bên, kẻ từ đỉnh của hình chóp xuống cạnh đáy).
Alt text: Minh họa công thức tính diện tích xung quanh của hình chóp tứ giác đều, với chú thích rõ ràng về các thành phần: diện tích xung quanh (Sxq), nửa chu vi đáy (p), và trung đoạn (d).
2. Thể Tích
Thể tích của hình chóp tứ giác đều được tính bằng công thức:
V = (1/3) * Sđáy * h
Trong đó:
Vlà thể tích của hình chóp.Sđáylà diện tích của mặt đáy (diện tích của hình vuông đáy).hlà chiều cao của hình chóp (khoảng cách từ đỉnh đến mặt đáy).
Alt text: Hình ảnh thể hiện công thức tính thể tích hình chóp tứ giác đều, làm nổi bật các yếu tố: thể tích (V), diện tích đáy (Sđáy), và chiều cao (h) của hình chóp.
Ví dụ:
Cho một hình chóp tứ giác đều có cạnh đáy bằng 6cm và chiều cao bằng 16cm. Thể tích của hình chóp là:
V = (1/3) * 6 * 6 * 16 = 192 cm³
Alt text: Hình ảnh minh họa bài toán tính thể tích hình chóp tứ giác đều, với các thông số cạnh đáy (6cm) và chiều cao (16cm) được ghi chú rõ ràng.
III. Bài Tập Vận Dụng
Câu 1: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = a, cạnh bên SA = b. Tính diện tích xung quanh và thể tích của hình chóp.
Lời giải:
- Diện tích đáy S.ABCD là:
a² - Gọi O là tâm của hình vuông ABCD, khi đó SO là đường cao của hình chóp.
- Tính SO dựa vào định lý Pitago trong tam giác vuông SOA:
SO = √(SA² - OA²) = √(b² - (a√2/2)²) = √(b² - a²/2) - Thể tích của hình chóp là:
V = (1/3) * a² * √(b² - a²/2) - Tính trung đoạn (chiều cao của mặt bên) dựa vào định lý Pitago hoặc công thức diện tích tam giác.
- Diện tích xung quanh là tổng diện tích 4 mặt bên (tam giác cân).
Câu 2: Một hình chóp tứ giác đều có thể tích bằng 100cm³, chiều cao hình chóp bằng 12cm. Tính diện tích đáy của hình chóp.
Lời giải:
- Sử dụng công thức tính thể tích:
V = (1/3) * Sđáy * h - Thay số vào:
100 = (1/3) * Sđáy * 12 - Giải phương trình để tìm Sđáy:
Sđáy = (100 * 3) / 12 = 25 cm²
Câu 3: Cho hình chóp tứ giác đều có cạnh đáy bằng 4cm, chiều cao của hình chóp là 9cm. Tính thể tích của hình chóp đó.
Lời giải:
- Diện tích đáy của hình chóp là: 4 * 4 = 16 cm²
- Thể tích của hình chóp là: V = (1/3) 16 9 = 48 cm³
Alt text: Hình ảnh mô phỏng hình chóp tứ giác đều trong bài toán thực tế, hỗ trợ việc hình dung và áp dụng công thức tính toán thể tích, diện tích.
Câu 4: Một cái lều hình chóp tứ giác đều có cạnh đáy là 3m và chiều cao là 2m. Tính thể tích không khí bên trong lều.
Lời giải:
- Diện tích đáy của lều là: 3 * 3 = 9 m²
- Thể tích không khí bên trong lều là: V = (1/3) 9 2 = 6 m³
Thông qua việc nắm vững định nghĩa, công thức và luyện tập các bài tập vận dụng, bạn sẽ hiểu rõ hơn về hình chóp tứ giác đều và ứng dụng được kiến thức này vào giải quyết các bài toán thực tế.