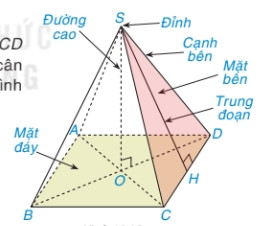
Hình Chóp Tứ Diện đều, một khái niệm quan trọng trong hình học không gian, không chỉ xuất hiện trong sách giáo khoa mà còn có nhiều ứng dụng thực tế thú vị. Bài viết này sẽ cung cấp một cái nhìn toàn diện về hình chóp tứ diện đều, từ định nghĩa, tính chất đến các công thức tính toán liên quan và các bài tập minh họa.
1. Định Nghĩa và Tính Chất Cơ Bản
Hình chóp tứ diện đều, hay còn gọi là tứ diện đều, là một loại hình chóp đặc biệt mà tất cả các mặt của nó đều là những tam giác đều bằng nhau. Nói cách khác, nó là một khối đa diện lồi có bốn mặt, và mỗi mặt là một tam giác đều.
Alt text: Mô hình trực quan về hình chóp tứ diện đều, thể hiện rõ các mặt tam giác đều đồng dạng, tối ưu cho hình học không gian lớp 11
Các tính chất quan trọng của hình chóp tứ diện đều:
- Tất cả bốn mặt đều là tam giác đều và bằng nhau.
- Tất cả sáu cạnh đều có độ dài bằng nhau.
- Mỗi đỉnh là giao điểm của ba mặt.
- Đường cao của hình chóp kẻ từ một đỉnh xuống mặt đối diện sẽ đi qua trọng tâm của tam giác đó.
2. Công Thức Tính Toán
Để giải các bài toán liên quan đến hình chóp tứ diện đều, chúng ta cần nắm vững các công thức tính toán sau:
-
Diện tích toàn phần (Stp): Vì hình chóp tứ diện đều có 4 mặt là tam giác đều bằng nhau, nên diện tích toàn phần sẽ bằng 4 lần diện tích của một mặt tam giác đều. Nếu cạnh của tứ diện đều là a, thì:
Stp = 4 * (a^2 * sqrt(3) / 4) = a^2 * sqrt(3) -
Thể tích (V): Thể tích của hình chóp tứ diện đều được tính bằng công thức:
V = (a^3 * sqrt(2)) / 12Trong đó, a là độ dài cạnh của tứ diện đều.
-
Độ dài đường cao (h): Đường cao của hình chóp tứ diện đều có thể được tính bằng công thức:
h = a * sqrt(6) / 3
3. Bài Tập Vận Dụng
Để hiểu rõ hơn về cách áp dụng các công thức trên, chúng ta hãy cùng xét một số bài tập ví dụ:
Bài tập 1: Cho hình chóp tứ diện đều ABCD có cạnh bằng 6cm. Tính diện tích toàn phần và thể tích của hình chóp.
Giải:
- Diện tích toàn phần:
Stp = 6^2 * sqrt(3) = 36 * sqrt(3) cm^2 - Thể tích:
V = (6^3 * sqrt(2)) / 12 = (216 * sqrt(2)) / 12 = 18 * sqrt(2) cm^3
Bài tập 2: Một hình chóp tứ diện đều có thể tích là 9 * sqrt(2) cm^3. Tính độ dài cạnh của hình chóp.
Giải:
- Ta có:
V = (a^3 * sqrt(2)) / 12 = 9 * sqrt(2) - Suy ra:
a^3 = (9 * sqrt(2) * 12) / sqrt(2) = 108 - Vậy:
a = cbrt(108) = 3 * cbrt(4) cm
4. Ứng Dụng Thực Tế
Hình chóp tứ diện đều không chỉ là một khái niệm trừu tượng trong toán học, mà còn có nhiều ứng dụng trong thực tế, ví dụ như:
- Kiến trúc: Hình dạng tứ diện đều được sử dụng trong thiết kế của một số công trình kiến trúc độc đáo, tạo nên vẻ đẹp hiện đại và ấn tượng.
- Khoa học vật liệu: Cấu trúc tứ diện đều xuất hiện trong một số cấu trúc tinh thể của vật liệu, ảnh hưởng đến tính chất vật lý và hóa học của chúng.
- Đồ chơi và trò chơi: Hình chóp tứ diện đều là một hình dạng phổ biến trong các loại đồ chơi lắp ghép và trò chơi trí tuệ, giúp phát triển tư duy không gian và khả năng sáng tạo.
Alt text: Ảnh cận cảnh lồng đèn hình chóp tứ giác đều, minh họa ứng dụng hình học trong trang trí nội thất và lễ hội truyền thống, tối ưu SEO cho từ khóa ‘lồng đèn hình chóp’
Kết luận:
Hình chóp tứ diện đều là một hình hình học không gian quan trọng với nhiều tính chất đặc biệt và ứng dụng thực tế. Việc nắm vững định nghĩa, tính chất và các công thức tính toán liên quan sẽ giúp chúng ta giải quyết các bài toán một cách dễ dàng và hiểu sâu sắc hơn về thế giới xung quanh. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về hình chóp tứ diện đều.