Hình Chóp Tam Giác Đều Là Gì? Khái Niệm, Đặc Điểm và Ứng Dụng

Hình chóp tam giác đều là một hình học không gian quen thuộc, xuất hiện nhiều trong chương trình Toán học và ứng dụng thực tế. Vậy Hình Chóp Tam Giác đều Là Gì? Bài viết này sẽ cung cấp một cái nhìn toàn diện về hình chóp tam giác đều, từ định nghĩa, đặc điểm, công thức tính toán đến các bài tập vận dụng.

Định Nghĩa Hình Chóp Tam Giác Đều

Hình chóp tam giác đều là một loại hình chóp đặc biệt, thỏa mãn các điều kiện sau:

• Đáy là tam giác đều: Tam giác đáy có ba cạnh bằng nhau và ba góc bằng 60 độ.
• Các mặt bên là các tam giác cân bằng nhau: Các mặt bên đều là hình tam giác cân và có chung một đỉnh. Đỉnh chung này là đỉnh của hình chóp.
• Đường cao: Đoạn thẳng nối đỉnh của hình chóp và trọng tâm của tam giác đáy được gọi là đường cao của hình chóp tam giác đều.

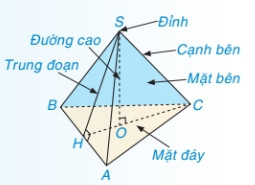Hình chóp tam giác đều với đáy là tam giác đều và các mặt bên là tam giác cân

Hình ảnh minh họa hình chóp tam giác đều, với đáy là tam giác đều và các mặt bên là các tam giác cân.

Các Yếu Tố Của Hình Chóp Tam Giác Đều

Một hình chóp tam giác đều bao gồm các yếu tố sau:

• Đỉnh (S): Điểm chung của tất cả các mặt bên.
• Mặt đáy (ABC): Tam giác đều nằm ở đáy của hình chóp.
• Mặt bên (SAB, SBC, SCA): Các tam giác cân có chung đỉnh S.
• Cạnh bên (SA, SB, SC): Các cạnh nối đỉnh S với các đỉnh của tam giác đáy.
• Cạnh đáy (AB, BC, CA): Các cạnh của tam giác đáy.
• Đường cao (SO): Đoạn thẳng vuông góc từ đỉnh S xuống mặt đáy, với O là trọng tâm của tam giác đáy.
• Trung đoạn (SI): Đường cao của mỗi mặt bên, kẻ từ đỉnh S xuống cạnh đáy của mặt bên đó.

Công Thức Tính Toán

Diện Tích Xung Quanh

Diện tích xung quanh của hình chóp tam giác đều là tổng diện tích của các mặt bên. Công thức tính như sau:

Sxq = p.d

Trong đó:

• Sxq là diện tích xung quanh.
• p là nửa chu vi đáy (nửa chu vi của tam giác đều).
• d là trung đoạn của hình chóp.

Công thức toán học thể hiện cách tính diện tích xung quanh của hình chóp tam giác đều.

Thể Tích

Thể tích của hình chóp tam giác đều được tính bằng một phần ba diện tích đáy nhân với chiều cao. Công thức như sau:

V = (1/3) S h

Trong đó:

• V là thể tích của hình chóp.
• S là diện tích đáy (diện tích của tam giác đều).
• h là chiều cao của hình chóp.

Công thức toán học thể hiện cách tính thể tích của hình chóp tam giác đều.

Bài Tập Vận Dụng

Để hiểu rõ hơn về hình chóp tam giác đều, chúng ta cùng xét một số bài tập vận dụng:

Bài tập 1: Cho hình chóp tam giác đều S.ABC có cạnh đáy AB = 6cm và trung đoạn SI = 5cm. Tính diện tích xung quanh của hình chóp.

Giải:

• Nửa chu vi đáy: p = (6 + 6 + 6) / 2 = 9 cm
• Diện tích xung quanh: Sxq = p d = 9 5 = 45 cm²

Bài tập 2: Cho hình chóp tam giác đều S.MNP có diện tích đáy là 15.6 cm² và chiều cao SH = 5cm. Tính thể tích của hình chóp.

Giải:

• Thể tích: V = (1/3) S h = (1/3) 15.6 5 = 26 cm³

Hình ảnh minh họa bài tập về hình chóp tam giác đều, giúp hình dung và giải bài tập dễ dàng hơn.

Ứng Dụng Thực Tế

Hình chóp tam giác đều không chỉ là một khái niệm toán học, mà còn xuất hiện trong nhiều ứng dụng thực tế, ví dụ:

• Kiến trúc: Mái nhà, chóp đỉnh của các công trình kiến trúc.
• Thiết kế: Các vật dụng trang trí, hộp quà, đồ chơi.
• Khoa học: Cấu trúc của một số tinh thể.

Kết Luận

Hình chóp tam giác đều là một hình học không gian thú vị với nhiều ứng dụng trong thực tế. Việc nắm vững định nghĩa, đặc điểm và công thức tính toán sẽ giúp bạn giải quyết các bài toán liên quan và hiểu rõ hơn về thế giới xung quanh. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về hình chóp tam giác đều.