Khái Niệm Về Hình Chóp Tam Giác
Hình Chóp Tam Giác là một hình đa diện được tạo thành bởi một mặt đáy là tam giác và ba mặt bên là các tam giác có chung một đỉnh. Đỉnh chung này được gọi là đỉnh của hình chóp.
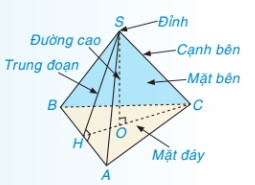Hình chóp tam giác đều minh họa các thành phần cơ bản như đỉnh, mặt đáy, và các mặt bên.
Hình chóp tam giác đều là một trường hợp đặc biệt của hình chóp tam giác, trong đó mặt đáy là một tam giác đều và các mặt bên là các tam giác cân bằng nhau.
Các yếu tố cơ bản của hình chóp tam giác:
- Đỉnh: Điểm chung của các mặt bên.
- Mặt đáy: Một tam giác.
- Mặt bên: Các tam giác nối đỉnh với các cạnh của mặt đáy.
- Cạnh bên: Các cạnh chung của các mặt bên.
- Đường cao: Đoạn thẳng nối đỉnh của hình chóp và trọng tâm của tam giác đáy, vuông góc với mặt đáy.
- Trung đoạn: Đường cao vẽ từ đỉnh của mỗi mặt bên.
Đặc Điểm Của Hình Chóp Tam Giác Đều
Hình chóp tam giác đều có những đặc điểm nổi bật sau:
- Đáy là tam giác đều.
- Mặt bên là các tam giác cân bằng nhau, có chung đỉnh.
- Chân đường cao kẻ từ đỉnh tới mặt đáy là điểm cách đều các đỉnh của tam giác đáy (trọng tâm của tam giác đều).
Công Thức Tính Diện Tích và Thể Tích
Diện tích xung quanh
Diện tích xung quanh của hình chóp tam giác đều bằng tích của nửa chu vi đáy với trung đoạn.
Công thức:
Trong đó:
p: nửa chu vi đáy.d: trung đoạn của hình chóp.
Thể tích
Thể tích của hình chóp tam giác đều bằng 1/3 tích của diện tích mặt đáy với chiều cao của nó.
Công thức:
Trong đó:
S: diện tích đáy.h: chiều cao của hình chóp.
Bài Tập Vận Dụng
Bài tập cơ bản
Ví dụ: Cho hình chóp tam giác đều S.ABC có cạnh đáy AB = 4cm, chiều cao SH = 6cm. Tính thể tích của hình chóp.
Giải:
- Tính diện tích đáy (tam giác đều ABC): S = (√3/4) a^2 = (√3/4) 4^2 = 4√3 cm².
- Tính thể tích hình chóp: V = (1/3) S h = (1/3) 4√3 6 = 8√3 cm³.
Bài tập nâng cao
Ví dụ: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên và mặt đáy bằng 60 độ. Tính thể tích của hình chóp.
Giải: (Bài tập này đòi hỏi kiến thức về góc giữa mặt phẳng và sử dụng các hệ thức lượng trong tam giác để tìm chiều cao).
Ứng Dụng Thực Tế Của Hình Chóp Tam Giác
Hình chóp tam giác không chỉ là một khái niệm toán học mà còn có nhiều ứng dụng trong thực tế:
- Kiến trúc: Thiết kế mái nhà, các công trình có hình dạng đặc biệt.
- Mỹ thuật: Tạo hình các tác phẩm điêu khắc, trang trí.
- Đóng gói: Thiết kế bao bì sản phẩm có hình dạng độc đáo, tiết kiệm vật liệu.
Bài Tập Thực Hành
Bài 1:
Cho hình chóp tam giác đều S.DEF, hãy xác định:
- Đỉnh của hình chóp.
- Các cạnh bên.
- Các mặt bên.
- Mặt đáy.
- Đường cao.
- Một trung đoạn.
Bài 2:
Cho hình chóp tam giác đều S.MNP có MN = NP = MP = 6 cm. Tam giác SNP cân tại S, SI là đường cao, SH là đường cao của hình chóp và SH = 5cm.
a) Tính diện tích tam giác MNP.
b) Tính thể tích hình chóp S.MNP.
Bài 3:
Một chiếc đèn trang trí có dạng hình chóp tam giác đều S.ABC, mỗi mặt là một tam giác đều có cạnh bằng 20 cm. Tính diện tích giấy màu cần dùng để làm đèn (bỏ qua diện tích các mối nối).
Thông qua bài viết này, hy vọng bạn đã nắm vững kiến thức về hình chóp tam giác, đặc biệt là hình chóp tam giác đều, cùng các công thức tính diện tích và thể tích liên quan. Hãy áp dụng những kiến thức này vào giải các bài tập và khám phá thêm những ứng dụng thú vị của hình chóp tam giác trong thực tế.
