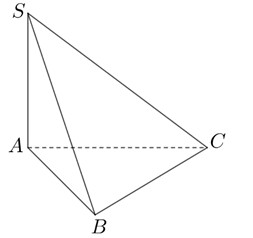
Hình Chóp SABC: Phân Tích Chi Tiết và Bài Tập Ứng Dụng

Hình Chóp Sabc là một trong những hình học không gian cơ bản và quan trọng trong chương trình toán học phổ thông. Bài viết này sẽ đi sâu vào các đặc điểm, công thức tính toán và các bài tập liên quan đến hình chóp SABC, giúp bạn nắm vững kiến thức và kỹ năng giải toán hiệu quả.

Định nghĩa hình chóp SABC:

Hình chóp SABC là hình chóp có đáy là tam giác ABC và đỉnh là điểm S nằm ngoài mặt phẳng chứa tam giác ABC.

Các yếu tố của hình chóp SABC:

• Đỉnh: S
• Mặt đáy: Tam giác ABC
• Các mặt bên: Tam giác SAB, tam giác SBC, tam giác SCA
• Các cạnh bên: SA, SB, SC
• Đường cao: Đường thẳng SH vuông góc với mặt phẳng (ABC), với H là chân đường cao.

Các dạng hình chóp SABC thường gặp:

1. Hình chóp SABC có cạnh bên SA vuông góc với mặt phẳng đáy (ABC): Đây là trường hợp đặc biệt, giúp đơn giản hóa việc tính toán và xác định các yếu tố hình học.

   Trong trường hợp này, SA chính là đường cao của hình chóp. Góc giữa cạnh bên SB và mặt phẳng (ABC) chính là góc SBA. Để tìm góc này, ta sử dụng các tỉ số lượng giác trong tam giác vuông SAB. Cụ thể, tan(SBA) = SA/AB. Bài toán thường cho các dữ kiện để tính SA và AB, từ đó suy ra góc SBA.

2. Hình chóp SABC đều: Là hình chóp có đáy ABC là tam giác đều và chân đường cao hạ từ đỉnh S xuống mặt đáy trùng với tâm của tam giác đều ABC.

3. Hình chóp SABC có các cạnh bên bằng nhau: Trong trường hợp này, hình chiếu của đỉnh S trên mặt phẳng đáy (ABC) là tâm đường tròn ngoại tiếp tam giác ABC.

Công thức tính thể tích hình chóp SABC:

Thể tích hình chóp SABC được tính theo công thức:

V = (1/3) S_đáy h

Trong đó:

• V là thể tích hình chóp
• S_đáy là diện tích mặt đáy (tam giác ABC)
• h là chiều cao của hình chóp (khoảng cách từ đỉnh S đến mặt phẳng đáy ABC)

Ví dụ minh họa và bài tập ứng dụng:

Ví dụ 1: Cho hình chóp SABC có SA vuông góc với mặt phẳng (ABC), SA = 2a, tam giác ABC vuông cân tại B và AC = 2a. Tính góc giữa đường thẳng SB và mặt phẳng (ABC).

Giải:

• Vì tam giác ABC vuông cân tại B và AC = 2a nên AB = BC = AC/√2 = a√2.
• Góc giữa SB và (ABC) là góc SBA.
• Trong tam giác vuông SAB, tan(SBA) = SA/AB = (2a)/(a√2) = √2.
• Vậy góc SBA = arctan(√2) ≈ 54.74 độ.

Ví dụ 2: Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC), SA = a√3. Tính thể tích hình chóp SABC.

Giải:

• Diện tích tam giác đều ABC là S_đáy = (a²√3)/4.
• Chiều cao của hình chóp là SA = a√3.
• Thể tích hình chóp SABC là V = (1/3) S_đáy h = (1/3) (a²√3)/4 a√3 = (a³)/4.

Để tính toán và giải quyết các bài toán liên quan đến hình chóp SABC, việc vẽ hình minh họa là vô cùng quan trọng. Nó giúp ta hình dung được các yếu tố, các mối quan hệ hình học và từ đó áp dụng các công thức một cách chính xác.

Việc xác định đúng đường cao, diện tích đáy và mối quan hệ giữa các yếu tố là chìa khóa để giải quyết các bài toán về thể tích và các yếu tố liên quan đến hình chóp SABC.

Bài tập tự luyện:

1. Cho hình chóp SABC có đáy ABC là tam giác vuông tại A, AB = a, AC = 2a, SA vuông góc với (ABC) và SA = a√5. Tính thể tích hình chóp SABC.
2. Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a, các cạnh bên SA = SB = SC = 2a. Tính khoảng cách từ A đến mặt phẳng (SBC).

Kết luận:

Hình chóp SABC là một chủ đề quan trọng trong hình học không gian. Việc nắm vững định nghĩa, các dạng hình chóp, công thức tính thể tích và các ví dụ minh họa sẽ giúp bạn tự tin giải quyết các bài tập liên quan. Hãy luyện tập thường xuyên để nâng cao kỹ năng và đạt kết quả tốt trong học tập.