Hình Chóp Có Các Cạnh Bên Bằng Nhau là một dạng hình học không gian đặc biệt và thường xuất hiện trong các bài toán liên quan đến hình học và tính thể tích. Bài viết này sẽ đi sâu vào tính chất, cách xác định và áp dụng công thức tính toán cho loại hình chóp này, kèm theo các ví dụ minh họa chi tiết.
1. Tính Chất Cơ Bản của Hình Chóp Có Các Cạnh Bên Bằng Nhau
Xét hình chóp S.A1A2…An có SA1 = SA2 = … = SAn. Khi đó:
-
Hình chiếu vuông góc: Hình chiếu vuông góc H của đỉnh S xuống mặt đáy (A1A2…An) trùng với tâm đường tròn ngoại tiếp đa giác đáy A1A2…An.
-
Trục ngoại tiếp: Đường thẳng SH là trục ngoại tiếp của đa giác đáy A1A2…An.
-
Công thức tính chiều cao: Nếu gọi R là bán kính đường tròn ngoại tiếp đa giác đáy và k là độ dài các cạnh bên bằng nhau (SA1 = SA2 = … = k), thì chiều cao h của hình chóp được tính theo công thức:
h = √(k² - R²)
2. Ứng Dụng vào Giải Bài Toán Thể Tích
Ví dụ 1: Cho hình chóp S.ABC có đáy là tam giác vuông tại A với AB = 1, AC = 2. Các cạnh bên SA = SB = SC = √3. Tính thể tích khối chóp S.ABC.
-
Bước 1: Tính diện tích đáy.
Diện tích tam giác ABC là: SABC = (1/2) AB AC = (1/2) 1 2 = 1.
-
Bước 2: Tính bán kính đường tròn ngoại tiếp đáy.
Vì tam giác ABC vuông tại A, nên bán kính đường tròn ngoại tiếp tam giác ABC là: R = BC/2 = √(AB² + AC²)/2 = √(1² + 2²)/2 = √5/2.
-
Bước 3: Tính chiều cao của hình chóp.
Do SA = SB = SC nên chiều cao h của hình chóp là: h = √(SA² – R²) = √(3 – (√5/2)²) = √(3 – 5/4) = √7/2.
-
Bước 4: Tính thể tích khối chóp.
Thể tích khối chóp S.ABC là: V = (1/3) SABC h = (1/3) 1 (√7/2) = √7/6.
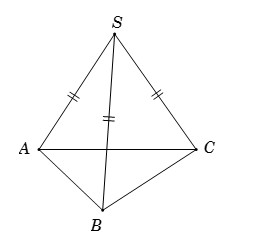Hình chóp S.ABC có đáy là tam giác vuông tại A, các cạnh bên SA, SB, SC bằng nhau và hình chiếu vuông góc của S xuống (ABC) là tâm đường tròn ngoại tiếp tam giác ABC
Ví dụ 2: Cho hình chóp S.ABC có SA = SB = AB = AC = a, SC = (√6/3)a. Mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Tính thể tích của khối chóp.
-
Phân tích: Bài toán này có thể được giải bằng cách xem hình chóp A.SBC có đỉnh là A. Vì AS = AB = AC nên hình chiếu vuông góc của A xuống mặt phẳng (SBC) là H, đồng thời H cũng là tâm đường tròn ngoại tiếp tam giác (SBC).
-
Bước 1: Xác định vị trí điểm H.
Do AB = AC và (SBC) vuông góc (ABC) nên suy ra H là trung điểm cạnh BC. Từ đó suy ra tam giác SBC vuông tại S.
-
Bước 2: Tính diện tích tam giác đáy SBC.
Diện tích tam giác SBC là: SSBC = (1/2) SB SC = (1/2) a (√6/3)a = (√6/6)a².
-
Bước 3: Tính bán kính đường tròn ngoại tiếp tam giác SBC.
Bán kính đường tròn ngoại tiếp tam giác SBC là: R = BC/2 = √(SB² + SC²)/2 = √(a² + (√6/3)²a²)/2 = √(15/9)a/2 = (√15/6)a.
-
Bước 4: Tính chiều cao của khối chóp A.SBC.
Chiều cao của khối chóp là: h = √(SA² – R²) = √(a² – ((√15/6)a)²) = √(a² – (15/36)a²) = √(21/36)a² = (√21/6)a.
-
Bước 5: Tính thể tích khối chóp A.SBC (tức S.ABC).
Thể tích khối chóp là: V = (1/3) SSBC h = (1/3) (√6/6)a² (√21/6)a = (√(621)/108)a³ = (√126/108)a³ = (√(914)/108)a³ = (3√14/108)a³ = (√14/36)a³.
Kết luận:
Hình chóp có các cạnh bên bằng nhau là một dạng hình đặc biệt với những tính chất hình học quan trọng. Việc nắm vững các tính chất này và công thức liên quan giúp giải quyết các bài toán tính thể tích một cách hiệu quả. Các ví dụ trên minh họa rõ ràng cách áp dụng lý thuyết vào thực tế, hỗ trợ người học hiểu sâu hơn về loại hình chóp này.
