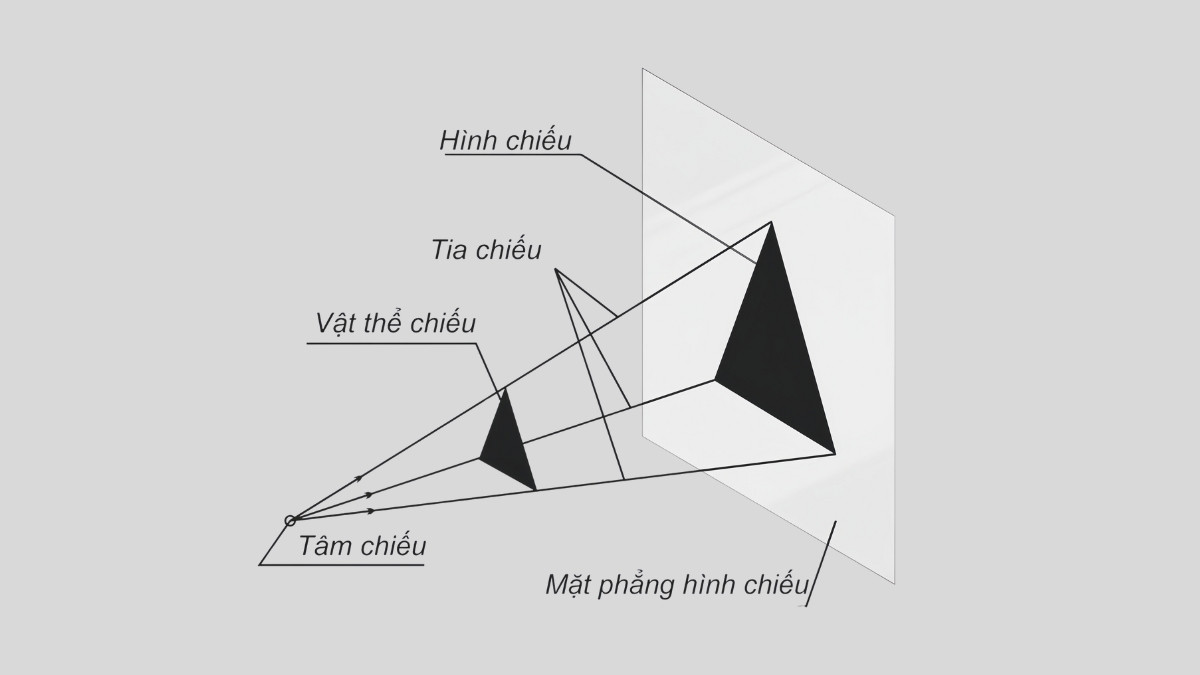
Hình chiếu là gì? Ứng dụng và phân loại trong toán học

Hình Chiếu Là một phương pháp biểu diễn các đối tượng ba chiều lên một mặt phẳng hai chiều. Khái niệm “hình chiếu là” vô cùng quan trọng trong toán học và vẽ kỹ thuật, cho phép chúng ta mô tả và phân tích các vật thể từ nhiều góc độ khác nhau. Để hiểu rõ hơn về điểm hình chiếu, hình chiếu cạnh hay hình chiếu bằng, hãy cùng khám phá chi tiết trong bài viết này.

Hình chiếu tạo ra một phiên bản “phẳng” của vật thể, cho phép đo đạc và phân tích dễ dàng hơn. Quá trình tạo ra một hình chiếu cần ba yếu tố: vật thể cần chiếu, mặt phẳng chiếu và phương pháp chiếu. Ví dụ, hình chiếu của một đoạn thẳng được xác định bởi khoảng cách từ hai điểm đầu mút của nó đến mặt phẳng chiếu, tạo thành góc 90 độ.

Hình chiếu là phương pháp biểu diễn vật thể ba chiều trên mặt phẳng hai chiều, giúp đơn giản hóa việc mô tả kích thước và hình dáng.

Phân loại hình chiếu và “hình chiếu là” gì trong toán học?

Trong toán học, “hình chiếu là” một phép biến đổi hình học quan trọng. Có hai loại hình chiếu chính: hình chiếu thẳng góc và hình chiếu trục đo.

Hình chiếu thẳng góc: Sử dụng các tia chiếu vuông góc với mặt phẳng chiếu. Ưu điểm của phương pháp này là bảo toàn kích thước và hình dạng của vật thể, giúp thể hiện chi tiết chính xác. Các hình chiếu thẳng góc cơ bản bao gồm:
- Hình chiếu đứng: Mô tả mặt trước của vật thể.
- Hình chiếu cạnh: Biểu diễn mặt bên của vật thể.
- Hình chiếu bằng: Mô tả phần trên của vật thể.
Hình chiếu trục đo: Cho phép biểu diễn cả ba chiều của vật thể trên cùng một mặt phẳng. Trong hình chiếu trục đo, các tia chiếu song song với nhau. Hình chiếu trục đo được chia thành hai loại chính:
- Trục đo vuông góc: Hệ số biến dạng có thể bằng nhau (đều), cân (hai trục bằng nhau) hoặc lệch (ba trục khác nhau).
- Trục đo xiên góc: Tương tự, có thể là xiên góc đều, cân hoặc lệch.

Ngoài ra, hình chiếu phối cảnh sử dụng các tia chiếu hội tụ về một hoặc nhiều điểm, tạo ra hiệu ứng không gian và chiều sâu. Các loại hình chiếu phối cảnh phổ biến là phối cảnh một điểm tụ, hai điểm tụ và ba điểm tụ, thường được sử dụng trong thiết kế và kiến trúc để tạo ra hình ảnh chân thực.

Hình chiếu thẳng góc giữ nguyên kích thước và hình dạng, trong khi hình chiếu trục đo và phối cảnh tạo ra hiệu ứng không gian ba chiều.

Tính chất quan trọng của “hình chiếu là” gì?

Để hiểu sâu hơn về “hình chiếu là” gì, chúng ta cần nắm vững các tính chất cơ bản của nó:

Tính xác định vị trí: Hình chiếu của một điểm trên một đường thẳng được xác định dựa trên đường thẳng đó. Nếu điểm nằm trên đường thẳng, hình chiếu của nó trùng với chính điểm đó.
Tính đồng hướng: Các điểm gần nhau trên một đường thẳng sẽ có hình chiếu gần nhau và nằm cùng phía trên đường thẳng chiếu.
Phạm vi: Hình chiếu của một điểm thuộc đoạn thẳng có thể nằm trên đoạn thẳng đó hoặc trên phần kéo dài của nó, tùy thuộc vào vị trí tương đối của điểm.
Bảo toàn khoảng cách: Khoảng cách giữa hai điểm được bảo toàn (hoặc tỉ lệ) so với khoảng cách giữa các hình chiếu tương ứng của chúng.
Tính vuông góc: Đường thẳng nối một điểm và hình chiếu của nó luôn vuông góc với mặt phẳng chiếu (trong trường hợp hình chiếu vuông góc).

Các tính chất này giúp ta xác định và phân tích mối quan hệ giữa vật thể gốc và hình chiếu của nó.

Các loại phép chiếu thường gặp và “hình chiếu là” gì?

Có ba loại phép chiếu chính, mỗi loại có ứng dụng và đặc điểm riêng:

Phép chiếu xuyên tâm: Các tia chiếu hội tụ tại một điểm duy nhất, gọi là tâm chiếu (S).
Phép chiếu song song: Các tia chiếu song song với nhau và với một hướng nhất định (L). Phép chiếu song song được sử dụng rộng rãi trong hình chiếu trục đo.
Phép chiếu vuông góc: Các tia chiếu song song và vuông góc với mặt phẳng chiếu.

Mỗi loại phép chiếu tạo ra một kiểu “hình chiếu là” khác nhau, phù hợp với các mục đích biểu diễn khác nhau.

“Hình chiếu vuông góc là” gì?

“Hình chiếu vuông góc là” hình chiếu mà đường nối từ một điểm đến mặt phẳng chiếu tạo thành một góc 90 độ với mặt phẳng đó. Nói cách khác, hình chiếu vuông góc của một điểm A lên mặt phẳng (Q) là điểm H sao cho đường thẳng AH vuông góc với (Q).

Các loại hình chiếu vuông góc phổ biến bao gồm:

Hình chiếu chính diện: Thể hiện vật thể từ phía trước.
Hình chiếu cạnh: Mô tả vật thể từ bên trái hoặc bên phải.
Hình chiếu từ trên xuống: Thể hiện hình dạng vật thể từ trên cao.

Hình chiếu vuông góc là một công cụ quan trọng trong kỹ thuật và thiết kế.

Cách tìm hình chiếu của một điểm lên đường thẳng, mặt phẳng

Để tìm hình chiếu của một điểm lên đường thẳng hoặc mặt phẳng, chúng ta thực hiện các bước sau:

Phương pháp giải

Tìm hình chiếu của điểm B lên đường thẳng d:
1. Xác định phương trình của mặt phẳng (P) đi qua B và vuông góc với d.
2. Tìm giao điểm H giữa đường thẳng d và mặt phẳng (P). Điểm H chính là hình chiếu của B lên d.
Tìm hình chiếu của điểm B lên mặt phẳng (P):
1. Lập phương trình của đường thẳng vuông góc với mặt phẳng (P) và đi qua B.
2. Tìm giao điểm H giữa đường thẳng vừa lập và mặt phẳng (P). Điểm H là hình chiếu của B lên (P).

Ví dụ minh họa

Xác định hình chiếu của điểm A(2,3,4) lên đường thẳng d: (x-1)/2 = (y+1)/1 = (z-2)/3

Giải:

Xác định phương trình mặt phẳng chứa điểm A:
- Đường thẳng d có vectơ chỉ phương u→=(2,1,3).
- Mặt phẳng (P) vuông góc với d sẽ nhận u→ làm vectơ pháp tuyến.
- Phương trình mặt phẳng (P): 2(x−2)+1(y−3)+3(z−4)=0 hay 2x+y+3z−19=0
Tìm giao điểm H của d với (P):
- Thay x=2t+1, y=t-1, z=3t+2 (phương trình tham số của d) vào phương trình mặt phẳng:
  2(2t+1)+(t-1)+3(3t+2) -19=0
  => 4t+2+t-1+9t+6-19=0
  => 14t – 12 = 0
  => t = 6/7
- Tọa độ H: x=2(6/7)+1=19/7, y=6/7-1=-1/7, z=3(6/7)+2=32/7
  => Điểm hình chiếu của A lên d là H(19/7; -1/7; 32/7)

Ví dụ này minh họa quy trình từng bước để tìm hình chiếu.

Hy vọng rằng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và chi tiết về “hình chiếu là” gì, cùng với các ứng dụng, phân loại và tính chất quan trọng của nó. Việc hiểu rõ về hình chiếu giúp chúng ta phân tích và biểu diễn các đối tượng trong không gian một cách dễ dàng và trực quan hơn, rất hữu ích trong nhiều lĩnh vực như toán học, kỹ thuật, thiết kế và kiến trúc.