Hệ Thức Lượng Giác Trong Tam Giác Vuông là một phần kiến thức quan trọng trong chương trình Toán lớp 9. Việc nắm vững các công thức và định lý sẽ giúp học sinh giải quyết các bài tập một cách hiệu quả và tự tin. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về các hệ thức lượng giác, kèm theo ví dụ minh họa và bài tập vận dụng.
1. Các Hệ Thức Lượng Giác Cơ Bản Trong Tam Giác Vuông
1.1. Hệ Thức Về Cạnh Và Đường Cao
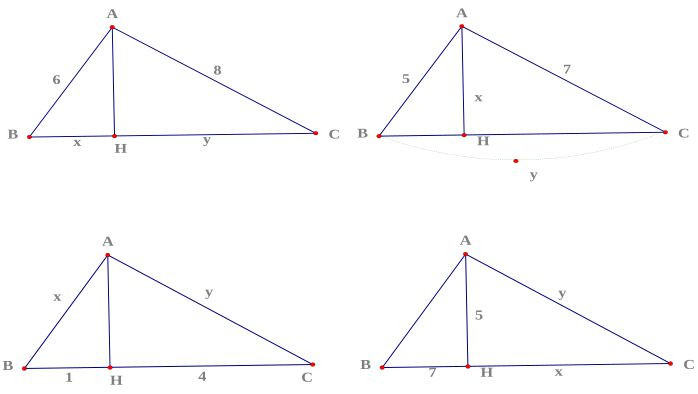
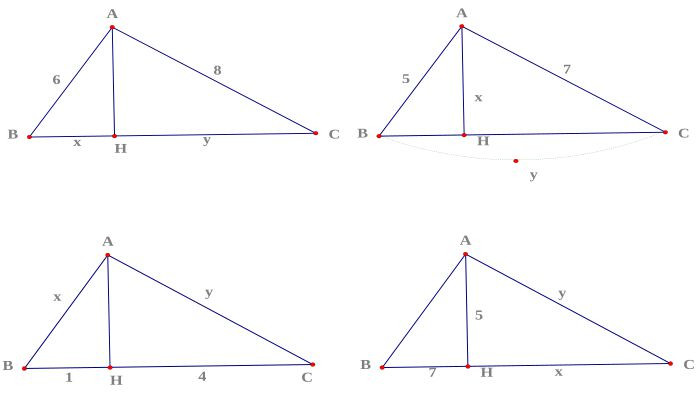
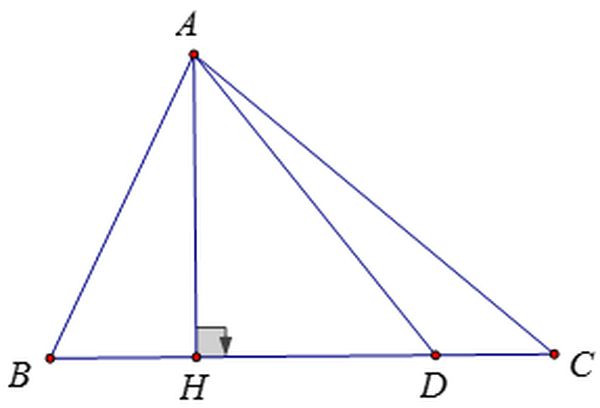
Xét tam giác ABC vuông tại A, với AH là đường cao. Ta có các hệ thức sau:
- Định lý 1 (Hệ thức 1):
AB² = BH * BC(Bình phương cạnh góc vuông bằng tích hình chiếu của cạnh đó trên cạnh huyền và cạnh huyền) - Định lý 2 (Hệ thức 2):
AC² = CH * BC(Tương tự như trên với cạnh góc vuông còn lại) - Định lý 3 (Hệ thức 3):
AH² = BH * CH(Bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền) - Định lý 4 (Hệ thức 4):
AB * AC = AH * BC(Tích hai cạnh góc vuông bằng tích của đường cao ứng với cạnh huyền và cạnh huyền) - Định lý 5 (Hệ thức 5):
1/AH² = 1/AB² + 1/AC²(Nghịch đảo bình phương đường cao bằng tổng các nghịch đảo bình phương của hai cạnh góc vuông) - Định lý Pythagoras:
BC² = AB² + AC²(Cạnh huyền bình phương bằng tổng bình phương hai cạnh góc vuông)
1.2. Tỉ Số Lượng Giác Của Góc Nhọn
Trong tam giác vuông ABC (vuông tại A), xét góc nhọn B (ký hiệu là α):
- Sinα (sin của góc α):
sinα = Đối / Huyền = AC / BC - Cosα (cosin của góc α):
cosα = Kề / Huyền = AB / BC - Tanα (tang của góc α):
tanα = Đối / Kề = AC / AB - Cotα (cotang của góc α):
cotα = Kề / Đối = AB / AC
Định lý về tỉ số lượng giác của hai góc phụ nhau:
Nếu hai góc α và β phụ nhau (α + β = 90°), thì:
sinα = cosβcosα = sinβtanα = cotβcotα = tanβ
So sánh giá trị lượng giác:
Cho hai góc nhọn α và β, với α < β:
sinα < sinβcosα > cosβtanα < tanβcotα > cotβ
2. Các Định Lý Lượng Giác Quan Trọng
Các định lý sau là sự hệ quả của các hệ thức trên và thường được sử dụng để giải bài tập:
- Định lý 1: Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền. (AB² = BH BC; AC² = CH BC)
- Định lý 2: Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền. (AH² = BH * CH)
- Định lý 3: Trong tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao ứng với cạnh huyền. (AB AC = AH BC)
- Định lý 4: Trong tam giác vuông, nghịch đảo bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo bình phương hai cạnh góc vuông. (1/AH² = 1/AB² + 1/AC²)
3. Bảng Giá Trị Lượng Giác Của Các Góc Đặc Biệt
Việc ghi nhớ bảng giá trị lượng giác của các góc đặc biệt (0°, 30°, 45°, 60°, 90°) là rất quan trọng để giải nhanh các bài toán.
| Góc α | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sinα | 0 | 1/2 | √2/2 | √3/2 | 1 |
| cosα | 1 | √3/2 | √2/2 | 1/2 | 0 |
| tanα | 0 | 1/√3 | 1 | √3 | Không xác định |
| cotα | Không xác định | √3 | 1 | 1/√3 | 0 |

4. Các Dạng Bài Tập Thường Gặp Và Phương Pháp Giải
4.1. Chứng Minh Hệ Thức Lượng Giác
- Phương pháp: Biến đổi một vế thành vế còn lại, hoặc biến đổi cả hai vế về một biểu thức chung. Sử dụng các hệ thức lượng giác cơ bản, định lý Pythagoras và các tính chất của tam giác vuông.
4.2. Tính Toán Các Đại Lượng Trong Tam Giác Vuông
- Phương pháp: Xác định các yếu tố đã biết và yếu tố cần tìm. Lựa chọn hệ thức lượng giác phù hợp để thiết lập phương trình. Giải phương trình để tìm ra kết quả.
4.3. Bài Toán Thực Tế
- Phương pháp: Đọc kỹ đề bài, vẽ hình minh họa. Xác định các yếu tố đã cho và yếu tố cần tìm. Áp dụng các hệ thức lượng giác để giải bài toán. Chú ý đến đơn vị đo.
5. Bài Tập Vận Dụng
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 4cm, CH = 9cm. Tính AB, AC, AH.
Giải:
- Áp dụng hệ thức
AH² = BH * CH=>AH² = 4 * 9 = 36=>AH = 6cm - Áp dụng hệ thức
AB² = BH * BC = BH * (BH + CH) = 4 * (4+9) = 52=>AB = √52 = 2√13 cm - Áp dụng hệ thức
AC² = CH * BC = CH * (BH + CH) = 9 * (4+9) = 117=>AC = √117 = 3√13 cm
Bài 2: Cho tam giác ABC vuông tại A, AB = 5cm, góc B = 60°. Tính AC, BC.
Giải:
tanB = AC / AB=>AC = AB * tanB = 5 * tan60° = 5√3 cmcosB = AB / BC=>BC = AB / cosB = 5 / cos60° = 5 / (1/2) = 10 cm
Bài 3: Một cột đèn cao 7m có bóng trên mặt đất dài 4m. Tính góc tạo bởi tia nắng mặt trời và mặt đất (làm tròn đến độ).
Giải:
- Gọi góc tạo bởi tia nắng mặt trời và mặt đất là α.
tanα = chiều cao cột đèn / độ dài bóng = 7 / 4α = arctan(7/4) ≈ 60°
Nắm vững các hệ thức lượng giác trong tam giác vuông sẽ giúp bạn tự tin giải quyết nhiều bài toán hình học và ứng dụng thực tế. Chúc các bạn học tốt!

