Định lý Thalet là một trong những định lý cơ bản và quan trọng trong hình học tam giác. Nó không chỉ giúp giải quyết các bài toán liên quan đến tỉ lệ đoạn thẳng mà còn là nền tảng cho nhiều khái niệm và định lý khác. Bài viết này sẽ đi sâu vào hệ quả của định lý Thalet trong tam giác, cùng các ứng dụng và bài tập minh họa.
1. Định Lý Thalet Đảo
Định lý Thalet đảo phát biểu rằng: “Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.”
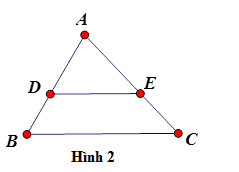
Hình ảnh minh họa định lý Thalet đảo: Nếu AD/DB = AE/EC thì DE song song BC.
Ví dụ: Trong tam giác ABC, nếu ta có AD/DB = AE/EC thì có thể kết luận DE // BC.
Ví dụ về định lý Thalet đảo: Tam giác ABC với AD/DB = AE/EC suy ra DE // BC.
2. Hệ Quả Của Định Lý Thalet
Hệ quả của định lý Thalet là một mở rộng quan trọng, giúp ta giải quyết nhiều bài toán phức tạp hơn. Hệ quả này phát biểu rằng: “Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.”
Hình ảnh minh họa hệ quả định lý Thalet: Nếu DE // BC thì AD/AB = AE/AC = DE/BC.
Ví dụ: Trong tam giác ABC, nếu DE // BC thì ta có các tỉ lệ sau: AD/AB = AE/AC = DE/BC. Điều này có nghĩa là tam giác ADE đồng dạng với tam giác ABC.
Minh họa hệ quả định lý Thalet: Tam giác ABC, DE // BC suy ra AD/AB = AE/AC = DE/BC.
Lưu ý: Hệ quả trên vẫn đúng trong trường hợp đường thẳng song song với một cạnh của tam giác và cắt phần kéo dài của hai cạnh còn lại.
Hệ quả mở rộng của định lý Thalet: Nếu BC // B’C’ thì AB’/AB = AC’/AC = B’C’/BC.
3. Ứng Dụng Của Hệ Quả Định Lý Thalet
Hệ quả định lý Thalet được ứng dụng rộng rãi trong giải toán hình học, đặc biệt là các bài toán liên quan đến:
- Tính độ dài đoạn thẳng: Khi biết tỉ lệ giữa các đoạn thẳng và độ dài một số đoạn, ta có thể tính được độ dài các đoạn còn lại.
- Chứng minh hai đường thẳng song song: Dựa vào định lý Thalet đảo, nếu chứng minh được tỉ lệ đoạn thẳng tương ứng bằng nhau thì có thể kết luận hai đường thẳng song song.
- Chứng minh các đẳng thức hình học: Sử dụng hệ quả định lý Thalet để thiết lập các tỉ lệ và từ đó suy ra các đẳng thức cần chứng minh.
- Tính chu vi, diện tích và các tỉ số liên quan: Khi tam giác mới được tạo ra đồng dạng với tam giác ban đầu, ta có thể sử dụng tỉ lệ đồng dạng để tính toán các đại lượng này.
4. Các Dạng Toán Thường Gặp Về Hệ Quả Định Lý Thalet
Dạng 1: Tính độ dài đoạn thẳng, chu vi, diện tích và các tỉ số
Phương pháp:
Sử dụng hệ quả định lý Thalet và tính chất của tỉ lệ thức để thiết lập các phương trình và giải chúng.
Ví dụ: Cho tam giác ABC, DE // BC (D thuộc AB, E thuộc AC). Biết AD = 4cm, DB = 6cm, BC = 15cm. Tính DE.
Giải:
Vì DE // BC, theo hệ quả định lý Thalet ta có:
AD/AB = DE/BC
=> 4/(4+6) = DE/15
=> DE = (4 * 15) / 10 = 6cm
Dạng 2: Chứng minh hai đường thẳng song song, chứng minh các đẳng thức hình học
Phương pháp:
Sử dụng định lý Thalet đảo và hệ quả định lý Thalet để chứng minh.
Ví dụ: Cho tam giác ABC, trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD/AB = AE/AC. Chứng minh rằng DE // BC.
Giải:
Theo giả thiết, ta có AD/AB = AE/AC. Áp dụng định lý Thalet đảo, ta kết luận DE // BC.
5. Bài Tập Vận Dụng
Bài 1: Cho hình vẽ, chọn câu sai:
Hình vẽ tam giác ABC, đường thẳng DE cắt AB, AC.
A. AD/AB = AE/AC => DE // BC
B. AD/DB = AE/EC => DE // BC
C. AB/DB = AC/EC => DE // BC
D. AD/DE = AE/ED => DE // BC
Đáp án: D (vì tỉ lệ AD/DE = AE/ED không đảm bảo DE // BC theo định lý Thalet đảo).
Bài 2: Cho hình vẽ, DE // BC, AD = 12, DB = 18, CE = 30. Tính AC.
Hình vẽ tam giác ABC, DE // BC, AD = 12, DB = 18, CE = 30.
Giải:
Vì DE // BC, theo định lý Thalet ta có:
AD/DB = AE/EC
12/18 = AE/30
=> AE = (12 * 30) / 18 = 20
Vậy, AC = AE + EC = 20 + 30 = 50
Đáp án: C. 50
Bài 3: Tính các độ dài x, y trong hình bên:
Hình ảnh tam giác vuông, cần tính x và y.
Giải:
Áp dụng định lý Py-ta-go và hệ quả định lý Thalet để tìm ra x và y. Kết quả là x = 5√5, y = 10.
Đáp án: D. x = 5√5, y = 10
Bài 4: Cho hình vẽ sau. Hỏi có bao nhiêu cặp đường thẳng song song?
Hình vẽ nhiều đường thẳng cắt nhau.
Giải:
Dựa vào tỉ lệ các đoạn thẳng, ta xác định được 3 cặp đường thẳng song song.
Đáp án: D. 3
Bài 5: Cho tứ giác ABCD có O là giao điểm của hai đường chéo. Đường thẳng qua A song song với BC cắt BD ở E. Đường thẳng qua B song song với AD cắt AC ở F. Chọn kết luận sai?
Đáp án: B. OE/OB = OA/OC
Định lý Thalet và hệ quả của nó là công cụ mạnh mẽ trong giải toán hình học. Việc nắm vững lý thuyết và luyện tập thường xuyên sẽ giúp bạn giải quyết các bài toán một cách dễ dàng và chính xác. Chúc các bạn học tốt!
Hình ảnh minh họa tính chất ba đường cao của tam giác.