Hệ Bất Phương Trình Bậc Nhất Hai Ẩn: Định Nghĩa, Cách Giải và Ứng Dụng

Hệ Bất Phương Trình Bậc Nhất Hai ẩn là một chủ đề quan trọng trong chương trình Toán lớp 10 và có nhiều ứng dụng thực tế. Bài viết này sẽ trình bày chi tiết về định nghĩa, cách giải và các ví dụ minh họa để giúp bạn nắm vững kiến thức này.

1. Định Nghĩa Bất Phương Trình Bậc Nhất Hai Ẩn

Bất phương trình bậc nhất hai ẩn là bất phương trình có dạng:

ax + by + c < 0
ax + by + c > 0
ax + by + c ≤ 0
ax + by + c ≥ 0

Trong đó:

a, b, c là các số thực đã cho, với điều kiện a² + b² ≠ 0.
x và y là các ẩn số.

Nghiệm của bất phương trình là cặp số (x₀; y₀) thỏa mãn bất phương trình đó. Ví dụ, cặp số (x₀; y₀) là nghiệm của ax + by + c < 0 nếu ax₀ + by₀ + c < 0. Các trường hợp khác được định nghĩa tương tự.

Alt text: Công thức toán học biểu diễn bất phương trình bậc nhất hai ẩn dạng ax + by + c < 0, thể hiện một trong các dạng cơ bản của bất phương trình.

2. Miền Nghiệm của Bất Phương Trình Bậc Nhất Hai Ẩn

2.1 Định nghĩa miền nghiệm

Miền nghiệm của một bất phương trình bậc nhất hai ẩn là tập hợp tất cả các điểm trên mặt phẳng tọa độ Oxy mà tọa độ của chúng là nghiệm của bất phương trình đó.

2.2 Cách biểu diễn miền nghiệm

Để biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn ax + by + c > 0 (hoặc <, ≤, ≥), ta thực hiện các bước sau:

Vẽ đường thẳng (d): ax + by + c = 0 trên mặt phẳng tọa độ.
Chọn một điểm M(x₀, y₀) không nằm trên đường thẳng (d). Thường chọn gốc tọa độ O(0;0) nếu nó không thuộc (d).
Thay tọa độ của M vào bất phương trình:
- Nếu ax₀ + by₀ + c > 0 (hoặc ≥ 0), thì nửa mặt phẳng chứa M (kể cả bờ nếu bất phương trình có dấu ≤ hoặc ≥) là miền nghiệm.
- Nếu ax₀ + by₀ + c < 0 (hoặc ≤ 0), thì nửa mặt phẳng không chứa M (kể cả bờ nếu bất phương trình có dấu ≤ hoặc ≥) là miền nghiệm.
Gạch bỏ phần không phải là miền nghiệm.

Lưu ý: Nếu bất phương trình có dấu ≤ hoặc ≥, thì miền nghiệm bao gồm cả đường thẳng (d). Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm.

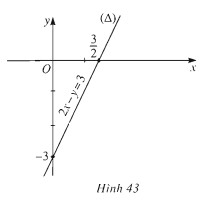
Ví dụ: Biểu diễn miền nghiệm của bất phương trình 2x - y ≤ 3.

Vẽ đường thẳng (Δ): 2x - y = 3.
Chọn điểm O(0; 0). Thay vào bất phương trình, ta có 2(0) - 0 = 0 ≤ 3.
Vậy, nửa mặt phẳng chứa gốc tọa độ là miền nghiệm của bất phương trình 2x - y ≤ 3.

Alt text: Hình ảnh minh họa miền nghiệm của bất phương trình bậc nhất hai ẩn 2x – y ≤ 3, là nửa mặt phẳng chứa gốc tọa độ.

3. Hệ Bất Phương Trình Bậc Nhất Hai Ẩn

3.1 Định nghĩa

Hệ bất phương trình bậc nhất hai ẩn là một tập hợp gồm hai hoặc nhiều bất phương trình bậc nhất hai ẩn.

3.2 Miền nghiệm

Miền nghiệm của hệ bất phương trình bậc nhất hai ẩn là tập hợp các điểm có tọa độ thỏa mãn tất cả các bất phương trình trong hệ. Nó chính là giao của các miền nghiệm của từng bất phương trình thành phần.

3.3 Cách xác định miền nghiệm

Để xác định miền nghiệm của hệ bất phương trình bậc nhất hai ẩn, ta thực hiện các bước sau:

Xác định miền nghiệm của từng bất phương trình trong hệ và gạch bỏ phần không phải là miền nghiệm.
Miền không bị gạch bỏ (phần còn lại sau khi đã gạch bỏ các miền không thỏa mãn) chính là miền nghiệm của hệ bất phương trình.

Ví dụ: Biểu diễn miền nghiệm của hệ bất phương trình:

{
  2x - y ≤ 3
  2x + 5y ≤ 12x + 8
}

Giải:

Đầu tiên, ta biến đổi hệ bất phương trình về dạng đơn giản hơn:

{
  2x - y ≤ 3
  -10x + 5y ≤ 8
}

Sau đó, ta vẽ các đường thẳng:

(d₁): 2x - y = 3 hay y = 2x - 3
(d₂): -10x + 5y = 8 hay y = 2x + 8/5

Lấy điểm O(0; 0), ta thấy O không thuộc cả hai đường thẳng và thỏa mãn cả hai bất phương trình. Do đó, miền nghiệm của hệ là miền được giới hạn bởi hai đường thẳng trên và chứa điểm O.

Alt text: Hình ảnh minh họa miền nghiệm của hệ bất phương trình bậc nhất hai ẩn, là phần mặt phẳng được giới hạn bởi hai đường thẳng và chứa gốc tọa độ.

4. Bài Tập Vận Dụng

4.1 Xác định miền nghiệm

Ví dụ 1: Tìm tập nghiệm của bất phương trình: -3x + 2y > 0

Alt text: Đồ thị biểu diễn miền nghiệm của bất phương trình -3x + 2y > 0 trên hệ trục tọa độ Oxy.

Ví dụ 2: Biểu diễn hình học tập nghiệm của hệ bất phương trình:

Alt text: Hình ảnh minh họa miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ.

4.2 Ứng dụng trong bài toán kinh tế

Hệ bất phương trình bậc nhất hai ẩn có nhiều ứng dụng trong thực tế, đặc biệt là trong các bài toán tối ưu hóa kinh tế.

Ví dụ 1: Một xưởng sản xuất hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm I cần 2 kg nguyên liệu và 30 giờ làm việc, lợi nhuận là 40,000 đồng. Để sản xuất một đơn vị sản phẩm II cần 4 kg nguyên liệu và 15 giờ làm việc, lợi nhuận là 30,000 đồng. Xưởng có 200 kg nguyên liệu và 120 giờ làm việc. Hãy lập kế hoạch sản xuất để lợi nhuận đạt được là lớn nhất.

Giải:

Gọi x là số đơn vị sản phẩm I, y là số đơn vị sản phẩm II cần sản xuất. Ta có bài toán tối ưu hóa:

Hàm mục tiêu (lợi nhuận): H(x, y) = 40000x + 30000y (cần cực đại hóa)
Ràng buộc:
- 2x + 4y ≤ 200 (nguyên liệu)
- 30x + 15y ≤ 1200 (thời gian)
- x ≥ 0, y ≥ 0 (số lượng sản phẩm không âm)

Bài toán này có thể giải bằng phương pháp đồ thị hoặc phương pháp đơn hình. Kết quả là xưởng nên sản xuất 20 đơn vị sản phẩm I và 40 đơn vị sản phẩm II để đạt lợi nhuận tối đa là 2,000,000 đồng.

Alt text: Đồ thị minh họa miền nghiệm của bài toán tối ưu hóa sản xuất với các ràng buộc về nguyên liệu và thời gian.

Hy vọng bài viết này đã cung cấp cho bạn cái nhìn tổng quan và chi tiết về hệ bất phương trình bậc nhất hai ẩn, từ định nghĩa, cách giải đến các ứng dụng thực tế. Chúc bạn học tốt!