1. Định nghĩa
Hàm Số Logarit là hàm số có dạng (y = {log _a}x), với cơ số (a) là một số dương khác 1 ((a > 0, a ne 1)).
2. Tính chất của hàm số logarit (y = {log _a}x) ((a > 0, a ne 1))
-
Tập xác định: ((0; +∞)). Hàm số logarit chỉ xác định với các giá trị dương của (x).
-
Đạo hàm: (forall x in (0; +∞), y’ = dfrac{1}{x ln a}). Đạo hàm này cho biết tốc độ thay đổi của hàm số logarit tại một điểm.
-
Chiều biến thiên:
-
Nếu (a > 1), hàm số luôn đồng biến trên tập xác định của nó. Điều này có nghĩa là khi (x) tăng, (y) cũng tăng.
-
Nếu (0 < a < 1), hàm số luôn nghịch biến trên tập xác định của nó. Điều này có nghĩa là khi (x) tăng, (y) giảm.
-
-
Tiệm cận: Trục (Oy) (trục tung) là tiệm cận đứng của đồ thị hàm số. Điều này có nghĩa là đồ thị hàm số tiến gần vô cùng đến trục (Oy) nhưng không bao giờ chạm vào nó.
-
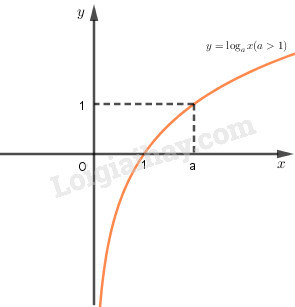
Đồ thị: Đồ thị của hàm số logarit nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm ((1; 0)) và đi qua điểm ((a; 1)).
Đồ thị hàm số logarit (y = log_a(x)) với (a > 1), minh họa tính đồng biến và tiệm cận đứng.
![Đồ thị hàm số logarit y=log_a(x) với 00, suy ra ((a^x)’ > 0, forall x) và (({log_a}^x)’ > 0, forall x > 0); do đó, hàm số mũ và hàm số logarit với cơ số lớn hơn 1 đều là các hàm số đồng biến.
Tương tự, nếu (0 < a < 1), thì (ln a < 0), suy ra ((a^x)’ < 0, forall x) và (({log_a}^x)’ < 0, forall x > 0); hàm số mũ và hàm số logarit với cơ số nhỏ hơn 1 đều là các hàm số nghịch biến.
- Công thức đạo hàm mở rộng:
((ln |x|)’ = dfrac{1}{x}, forall x ne 0) và ((log_a |x|)’ = frac{1}{x ln a}, forall x ne 0.)
Hình ảnh minh họa mối quan hệ giữa hàm số mũ và hàm số logarit, thể hiện tính chất nghịch đảo và hình dạng đồ thị tương ứng.
5. Bài tập về hàm số logarit
Bài 1. Tìm tập xác định (D) của hàm số (y = log_{sqrt{2}} left( frac{-3}{2 – 2x} right)).
A. (D = (-infty; 1))
B. (D = [1; +infty))
C. (D = (-infty; 1])
D. (D = (1; +infty))
Lời giải:
Điều kiện để hàm số xác định là biểu thức trong logarit phải lớn hơn 0:
(frac{-3}{2 – 2x} > 0)
Vì (-3 < 0), để phân số dương thì mẫu phải âm:
(2 – 2x < 0 Leftrightarrow 2x > 2 Leftrightarrow x > 1)
Vậy tập xác định là (D = (1; +infty)).
Chọn đáp án D.
Bài 2. Cho (a, b) là các số thực, thỏa mãn (0 < a A. (log_b a + log_a b < 0)
B. (log_b a > 1)
C. (log_a b > 0)
D. (log_a b + log_b a ge 2)
Lời giải:
Vì (0 < a < 1) nên (log_a b < 0).
Vì (b > 1) nên hàm số (y = log_b x) đồng biến, do đó (a < b) nên (log_b a < log_b b = 1).
Vậy (log_a b < 0) và (log_b a < 1)
Chọn đáp án A.
Bài 3. Đạo hàm của hàm số (y = log_{2018}(2018x + 1)) là:
A. (frac{1}{x ln 2018})
B. (frac{2018}{2018(x + 1) ln 2018})
C. (frac{1}{(2018x + 1) ln 2018})
D. (frac{2018}{(2018x + 1) ln 2018})
Lời giải:
Sử dụng công thức đạo hàm của hàm logarit cơ số a:
((log_a u)’ = frac{u’}{u ln a})
Trong trường hợp này, (u = 2018x + 1) và (a = 2018), ta có:
(y’ = frac{(2018x + 1)’}{(2018x + 1) ln 2018} = frac{2018}{(2018x + 1) ln 2018})
Chọn đáp án D.
Bài 4. Gọi ((C)) là đồ thị hàm số (y = log x). Tìm khẳng định đúng?
A. Đồ thị ((C)) có tiệm cận đứng.
B. Đồ thị ((C)) có tiệm cận ngang.
C. Đồ thị ((C)) cắt trục tung.
D. Đồ thị ((C)) không cắt trục hoành.
Lời giải:
-
Đồ thị hàm số (y = log x) nhận trục tung làm tiệm cận đứng.
-
Đồ thị hàm số không có tiệm cận ngang và cắt trục hoành tại điểm ((1; 0)) nên các đáp án B, C, D đều sai.
Chọn đáp án A.