1. Định nghĩa hàm số logarit
Hàm Số Logarit là hàm số có dạng (y = log_a x), trong đó (a) là cơ số, là một số dương khác 1 ((a > 0, a ne 1)). Hàm số logarit là hàm ngược của hàm số mũ (y = a^x). Việc nghiên cứu hàm số logarit giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các đại lượng biến thiên theo quy luật mũ.
2. Tính chất của hàm số logarit (y = log_a x)
2.1. Tập xác định
Hàm số logarit (y = log_a x) chỉ xác định khi (x > 0). Do đó, tập xác định của hàm số logarit là khoảng ((0; +∞)).
2.2. Đạo hàm
Đạo hàm của hàm số logarit (y = log_a x) là (y’ = dfrac{1}{x ln a}) với mọi (x ∈ (0; +∞)). Đạo hàm này cho biết tốc độ thay đổi của hàm số tại một điểm.
2.3. Chiều biến thiên
Chiều biến thiên của hàm số logarit phụ thuộc vào giá trị của cơ số (a):
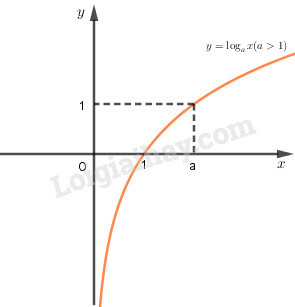
- Nếu (a > 1), hàm số (y = log_a x) đồng biến trên khoảng ((0; +∞)). Điều này có nghĩa là khi (x) tăng, (y) cũng tăng.
- Nếu (0 < a < 1), hàm số (y = log_a x) nghịch biến trên khoảng ((0; +∞)). Điều này có nghĩa là khi (x) tăng, (y) giảm.
Alt text: Đồ thị hàm số logarit y = log_a(x) với a > 1, thể hiện tính chất đồng biến và đi qua điểm (1,0)
2.4. Tiệm cận
Trục (Oy) (trục tung) là tiệm cận đứng của đồ thị hàm số (y = log_a x). Điều này có nghĩa là đồ thị hàm số tiến gần vô cùng đến trục tung khi (x) tiến gần đến 0.
2.5. Đồ thị
Đồ thị của hàm số logarit (y = log_a x) nằm hoàn toàn phía bên phải trục tung. Đồ thị luôn cắt trục hoành tại điểm ((1; 0)) và đi qua điểm ((a; 1)). Hình dạng của đồ thị phụ thuộc vào giá trị của cơ số (a):
- Nếu (a > 1), đồ thị đi lên từ trái sang phải.
- Nếu (0 < a < 1), đồ thị đi xuống từ trái sang phải.
Alt text: Đồ thị hàm số logarit y = log_a(x) với 0 < a < 1, thể hiện tính chất nghịch biến và tiệm cận đứng là trục Oy
3. Các công thức logarit quan trọng
Để giải các bài toán liên quan đến hàm số logarit, chúng ta cần nắm vững các công thức sau:
- (log_a (xy) = log_a x + log_a y)
- (log_a left(dfrac{x}{y}right) = log_a x – log_a y)
- (log_a x^alpha = alpha log_a x)
- (log_a b = dfrac{log_c b}{log_c a}) (công thức đổi cơ số)
- (a^{log_a x} = x)
- (log_a a = 1)
- (log_a 1 = 0)
4. Ứng dụng của hàm số logarit
Hàm số logarit có nhiều ứng dụng trong các lĩnh vực khác nhau, bao gồm:
- Toán học: Giải các phương trình và bất phương trình mũ và logarit.
- Vật lý: Tính độ lớn của các đại lượng như cường độ âm (dB), độ pH.
- Hóa học: Tính hằng số cân bằng, tốc độ phản ứng.
- Tin học: Phân tích độ phức tạp của thuật toán (O(log n)).
- Tài chính: Tính lãi suất kép, giá trị hiện tại và tương lai của dòng tiền.
- Địa chất: Xác định tuổi của các mẫu vật bằng phương pháp đồng vị phóng xạ.
5. Bài tập ví dụ về hàm số logarit
Bài 1: Tìm tập xác định của hàm số (y = log_2 (x – 3)).
Giải:
Hàm số xác định khi (x – 3 > 0) hay (x > 3). Vậy tập xác định là (D = (3; +∞)).
Bài 2: Tính đạo hàm của hàm số (y = log_3 (2x + 1)).
Giải:
Ta có (y’ = dfrac{(2x + 1)’}{(2x + 1) ln 3} = dfrac{2}{(2x + 1) ln 3}).
Bài 3: Giải phương trình (log_2 (x + 1) + log_2 (x – 1) = 3).
Giải:
Điều kiện: (x > 1).
Phương trình tương đương với (log_2 [(x + 1)(x – 1)] = 3) hay ((x + 1)(x – 1) = 2^3 = 8).
Suy ra (x^2 – 1 = 8) hay (x^2 = 9).
Vậy (x = 3) (thỏa mãn điều kiện) hoặc (x = -3) (loại).
Bài 4. Cho hàm số (y = log_a x) có đồ thị đi qua điểm (A(4; 2)). Tìm (a).
Giải:
Thay tọa độ điểm A vào phương trình hàm số, ta có (2 = log_a 4) hay (a^2 = 4).
Vì (a > 0) và (a ne 1) nên (a = 2).
Bài 5. Tìm khoảng đồng biến của hàm số (y = log_{0.5} (x^2 + 1)).
Giải:
Xét hàm số (u = x^2 + 1), ta có (u’ = 2x).
Hàm số (y = log_{0.5} u) nghịch biến vì (0 < 0.5 < 1).
Do đó, hàm số (y = log_{0.5} (x^2 + 1)) đồng biến khi (u’ < 0) hay (2x < 0) suy ra (x < 0).
Vậy hàm số đồng biến trên khoảng ((-infty; 0)).
Alt text: Hình ảnh minh họa về ứng dụng của hàm số mũ và logarit trong các lĩnh vực khoa học và đời sống, thể hiện sự tăng trưởng và suy giảm
6. Kết luận
Hàm số logarit là một công cụ toán học mạnh mẽ với nhiều ứng dụng thực tế. Việc nắm vững định nghĩa, tính chất và các công thức liên quan đến hàm số logarit sẽ giúp chúng ta giải quyết các bài toán và hiểu rõ hơn về thế giới xung quanh. Việc luyện tập thường xuyên với các bài tập đa dạng sẽ giúp bạn củng cố kiến thức và áp dụng chúng một cách linh hoạt.