Hàm Cos (hay cosine) là một khái niệm toán học quan trọng, đặc biệt trong lượng giác. Nó không chỉ là một công cụ để giải quyết các bài toán hình học mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khoa học và kỹ thuật. Bài viết này sẽ cung cấp một cái nhìn toàn diện về hàm cos, từ định nghĩa cơ bản đến các ứng dụng nâng cao, phù hợp cho học sinh và những ai quan tâm đến toán học.
Định Nghĩa Hàm Cos
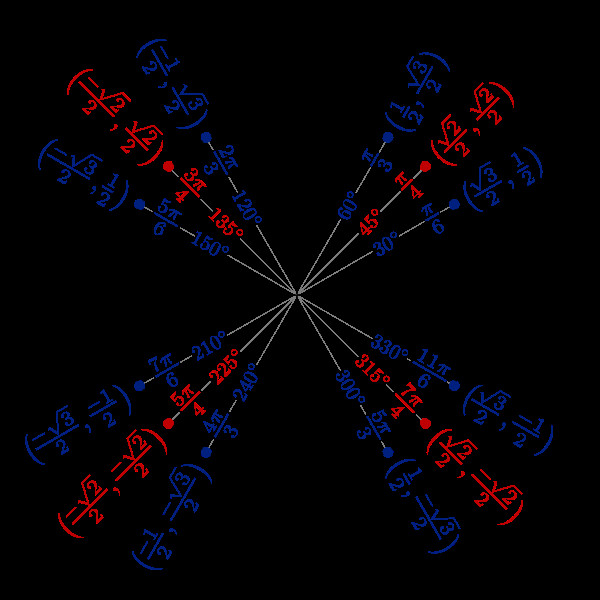
Trong một tam giác vuông, cosin của một góc nhọn được định nghĩa là tỷ số giữa cạnh kề và cạnh huyền. Mở rộng ra, trong đường tròn lượng giác, cosin của một góc là hoành độ của điểm trên đường tròn tương ứng với góc đó.
Đường tròn lượng giác với các giá trị góc và cosin tương ứng, thể hiện mối quan hệ giữa góc và hoành độ trên đường tròn.
Định Lý Hàm Cos
Định lý hàm cos (còn gọi là định lý cosin) là một mở rộng của định lý Pythagoras cho các tam giác bất kỳ. Nó thiết lập mối quan hệ giữa độ dài các cạnh của một tam giác và cosin của một trong các góc của nó.
Phát biểu định lý: Trong một tam giác ABC với các cạnh a, b, c và góc A đối diện với cạnh a, ta có:
a² = b² + c² – 2bc * cosA
Tương tự, ta cũng có:
- b² = a² + c² – 2ac * cosB
- c² = a² + b² – 2ab * cosC
Định lý này cho phép tính độ dài một cạnh của tam giác nếu biết độ dài hai cạnh còn lại và góc xen giữa. Hoặc, nếu biết độ dài ba cạnh, có thể tính được các góc của tam giác.
Công thức tổng quát của định lý hàm cos, thể hiện mối liên hệ giữa các cạnh và góc trong một tam giác.
Chứng Minh Định Lý Hàm Cos
Có nhiều cách để chứng minh định lý hàm cos, một trong những cách phổ biến nhất là sử dụng hình học và định lý Pythagoras.
Cách chứng minh:
- Vẽ đường cao: Từ đỉnh A của tam giác ABC, vẽ đường cao AH vuông góc với cạnh BC.
- Áp dụng định lý Pythagoras: Xét hai tam giác vuông ABH và ACH, áp dụng định lý Pythagoras.
- Sử dụng tỉ số lượng giác: Biểu diễn AH và BH (hoặc CH) theo các cạnh và góc của tam giác ABC, sử dụng các tỉ số lượng giác cơ bản (sin, cos).
- Biến đổi đại số: Thực hiện các phép biến đổi đại số để thu được công thức của định lý hàm cos.
Một cách khác để chứng minh là sử dụng tọa độ Descartes, bằng cách biểu diễn các đỉnh của tam giác bằng tọa độ và sử dụng công thức khoảng cách và công thức tính cosin của góc giữa hai vectơ.
Ứng Dụng của Hàm Cos và Định Lý Hàm Cos
Hàm cos và định lý hàm cos có nhiều ứng dụng quan trọng trong toán học và các lĩnh vực liên quan:
- Giải tam giác: Tính các cạnh và góc còn lại của một tam giác khi biết một số thông tin về cạnh và góc.
- Tính khoảng cách: Trong trắc địa và định vị, định lý hàm cos được sử dụng để tính khoảng cách giữa các điểm trên bề mặt trái đất.
- Vật lý: Trong cơ học, hàm cos được sử dụng để phân tích các lực và chuyển động, đặc biệt là trong dao động điều hòa và sóng.
- Kỹ thuật: Trong xây dựng và thiết kế, hàm cos được sử dụng để tính toán các góc và khoảng cách, đảm bảo tính chính xác của các công trình.
- Điều hướng: Trong hàng hải và hàng không, định lý hàm cos được sử dụng để tính toán vị trí và hướng đi.
Phân tích lực tác dụng lên một vật thể sử dụng hàm cos để tính thành phần của lực theo các phương khác nhau.
Hàm Cos trong Chương Trình Toán Học
Trong chương trình toán học phổ thông, hàm cos và định lý hàm cos thường được giới thiệu ở lớp 9, trong phần hình học và lượng giác. Học sinh sẽ được học về định nghĩa, tính chất và ứng dụng của hàm cos để giải các bài toán liên quan đến tam giác và các hình học khác.
Việc nắm vững kiến thức về hàm cos là rất quan trọng, vì nó là nền tảng cho việc học các khái niệm lượng giác phức tạp hơn ở các lớp trên, cũng như ứng dụng vào các môn khoa học khác.
Kết Luận
Hàm cos là một công cụ toán học mạnh mẽ với nhiều ứng dụng thực tế. Hiểu rõ định nghĩa, tính chất và ứng dụng của hàm cos sẽ giúp học sinh và những người quan tâm đến toán học giải quyết các bài toán một cách hiệu quả và khám phá thêm nhiều điều thú vị trong thế giới xung quanh.