Hàm chẵn và hàm lẻ là những khái niệm quan trọng trong toán học, đặc biệt là khi học về hàm số ở lớp 10. Việc hiểu rõ định nghĩa, tính chất và cách xác định hàm chẵn, hàm lẻ giúp học sinh dễ dàng hơn trong việc giải các bài toán liên quan và xây dựng nền tảng vững chắc cho các kiến thức toán học nâng cao sau này.
1. Định Nghĩa Hàm Chẵn và Hàm Lẻ
Cho hàm số $y = f(x)$ xác định trên tập hợp Q (tập xác định).
-
Hàm số chẵn: $f(x)$ được gọi là hàm số chẵn nếu thỏa mãn hai điều kiện sau:
- Với mọi $x in Q$, thì $-x in Q$ (tập xác định đối xứng).
- $f(-x) = f(x)$ với mọi $x in Q$.
-
Hàm số lẻ: $f(x)$ được gọi là hàm số lẻ nếu thỏa mãn hai điều kiện sau:
- Với mọi $x in Q$, thì $-x in Q$ (tập xác định đối xứng).
- $f(-x) = -f(x)$ với mọi $x in Q$.
Lưu ý:
- Tập xác định Q phải là một tập đối xứng, nghĩa là nếu $x$ thuộc Q thì $-x$ cũng phải thuộc Q.
- Một hàm số có thể không phải là hàm chẵn cũng không phải là hàm lẻ. Những hàm số như vậy được gọi là hàm số “không chẵn không lẻ”.
2. Đặc Điểm Đồ Thị Hàm Chẵn và Hàm Lẻ
Đồ thị của hàm số chẵn và hàm số lẻ có những đặc điểm đối xứng riêng biệt, giúp chúng ta nhận biết chúng một cách trực quan.
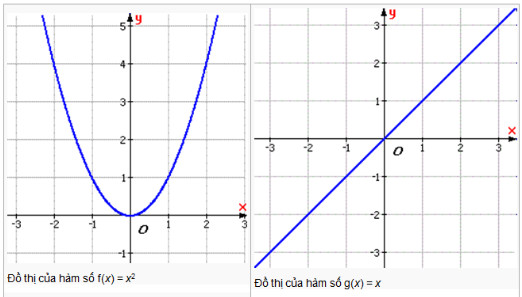
- Hàm số chẵn: Đồ thị của hàm số chẵn nhận trục tung (Oy) làm trục đối xứng. Điều này có nghĩa là, nếu bạn gấp đồ thị theo trục tung, hai nửa của đồ thị sẽ trùng khớp với nhau.
- Hàm số lẻ: Đồ thị của hàm số lẻ nhận gốc tọa độ (O) làm tâm đối xứng. Điều này có nghĩa là, nếu bạn quay đồ thị 180 độ quanh gốc tọa độ, đồ thị sẽ không thay đổi.
Ví dụ:
- Hàm số $y = x^2$ là hàm số chẵn và đồ thị của nó đối xứng qua trục tung.
- Hàm số $y = x$ là hàm số lẻ và đồ thị của nó đối xứng qua gốc tọa độ.
Một số hàm số không có tính chất đối xứng và không phải là hàm chẵn cũng không phải là hàm lẻ.
3. Các Bước Xác Định Tính Chẵn Lẻ của Hàm Số
Để xét tính chẵn lẻ của một hàm số $y = f(x)$ xác định trên tập xác định Q, chúng ta thực hiện theo các bước sau:
Bước 1: Tìm tập xác định Q của hàm số. Xác định rõ ràng tập xác định của hàm số là bước đầu tiên và quan trọng.
Bước 2: Kiểm tra tính đối xứng của tập xác định.
- Nếu tồn tại một giá trị $x_0$ thuộc Q, mà $-x_0$ không thuộc Q, thì kết luận ngay hàm số không chẵn và không lẻ.
- Nếu với mọi $x$ thuộc Q, ta có $-x$ cũng thuộc Q (tập xác định đối xứng), thì chuyển sang bước 3.
Bước 3: Tính $f(-x)$ và so sánh với $f(x)$.
- Nếu $f(-x) = f(x)$ với mọi $x$ thuộc Q, kết luận hàm số là hàm số chẵn.
- Nếu $f(-x) = -f(x)$ với mọi $x$ thuộc Q, kết luận hàm số là hàm số lẻ.
- Nếu không thỏa mãn cả hai điều kiện trên, kết luận hàm số không chẵn và không lẻ.
Ví dụ minh họa:
Ví dụ 1: Xét tính chẵn lẻ của hàm số $f(x) = 3x^3 + 2sqrt[3]{x}$.
- Tập xác định: $D = mathbb{R}$ (tập số thực).
- Với mọi $x in mathbb{R}$, ta có $-x in mathbb{R}$.
- $f(-x) = 3(-x)^3 + 2sqrt[3]{-x} = -3x^3 – 2sqrt[3]{x} = -(3x^3 + 2sqrt[3]{x}) = -f(x)$.
Kết luận: Hàm số $f(x) = 3x^3 + 2sqrt[3]{x}$ là hàm số lẻ.
Ví dụ 2: Xét tính chẵn lẻ của hàm số $f(x) = x^4 + sqrt{x^2 + 1}$.
- Tập xác định: $D = mathbb{R}$ (tập số thực).
- Với mọi $x in mathbb{R}$, ta có $-x in mathbb{R}$.
- $f(-x) = (-x)^4 + sqrt{(-x)^2 + 1} = x^4 + sqrt{x^2 + 1} = f(x)$.
Kết luận: Hàm số $f(x) = x^4 + sqrt{x^2 + 1}$ là hàm số chẵn.
Ví dụ 3: Xét tính chẵn lẻ của hàm số $f(x) = sqrt{2 + x} + frac{1}{sqrt{2 – x}}$.
-
Điều kiện xác định:
- $2 + x geq 0 Rightarrow x geq -2$
- $2 – x > 0 Rightarrow x < 2$
-
Tập xác định: $D = [-2; 2)$.
-
Ta thấy rằng $x_0 = -2 in D$, nhưng $-x_0 = 2 notin D$.
Kết luận: Hàm số $f(x) = sqrt{2 + x} + frac{1}{sqrt{2 – x}}$ không chẵn và không lẻ.
4. Bài Tập Vận Dụng
Để củng cố kiến thức, chúng ta cùng luyện tập với một số bài tập sau:
Câu 1: Xét tính chẵn lẻ của hàm số $y = f(x) = frac{sqrt{1-x} – sqrt{1+x}}{|x-1| – |1+x|}$.
Câu 2: Xét tính chẵn lẻ của hàm số $f(x) = x^4 – 4x – 2$.
Câu 3: Xét tính chẵn lẻ của hàm số sau:
Câu 4: Xét tính chẵn lẻ của hàm số $y = x$.
Câu 5: Tìm $m$ để hàm số sau là hàm số chẵn:
Hướng dẫn giải:
Câu 1:
Câu 2:
- Tập xác định: $D = mathbb{R}$.
- Với mọi $x in mathbb{R}$, ta có $-x in mathbb{R}$.
- $f(-x) = (-x)^4 – 4(-x) – 2 = x^4 + 4x – 2$.
Kết luận: Hàm số không chẵn và không lẻ.
Câu 3:
- Tập xác định: $D = mathbb{R}$.
- Với mọi $x in mathbb{R}$, ta có $-x in mathbb{R}$.
- Với mọi $x > 0$ ta có $-x < 0$ => $f(-x) = -1$, $f(x) = 1$ => $f(-x) = -f(x)$
- Với mọi $x < 0$ => $f(-x) = 1$, $f(x) = -1$ => $f(-x) = -f(x)$
- Và $f(-0) = -f(0) = 0$
Do đó với mọi $x in mathbb{R}$ ta có $f(-x) = -f(x)$. Vậy hàm số là hàm lẻ.
Câu 4:
- Đặt $y = f(x) = x$.
- Tập xác định: $D = mathbb{R}$ => với mọi $x in D$ thì $-x in D$.
- Ta có: $f(-x) = -x = -f(x)$.
Vậy hàm số $y = x$ là hàm số lẻ.
Câu 5:
Kết Luận
Hiểu rõ về hàm chẵn, hàm lẻ là một phần quan trọng trong chương trình Toán lớp 10. Bài viết này đã cung cấp đầy đủ kiến thức về định nghĩa, tính chất, cách nhận biết và các bài tập vận dụng liên quan đến hàm chẵn và hàm lẻ. Việc nắm vững các kiến thức này sẽ giúp học sinh tự tin hơn trong việc giải các bài toán và xây dựng nền tảng vững chắc cho các kiến thức toán học sau này.