Vectơ là một khái niệm cơ bản trong toán học và vật lý, mô tả một đoạn thẳng có hướng. Hiểu rõ về vectơ, đặc biệt là khi nào Hai Vectơ Cùng Hướng, là nền tảng để giải quyết nhiều bài toán liên quan.
1. Định Nghĩa Vectơ
Vectơ là một đoạn thẳng có hướng, được xác định bởi điểm đầu và điểm cuối. Vectơ ký hiệu là , với A là điểm đầu và B là điểm cuối. Vectơ này biểu diễn sự di chuyển từ A đến B.
2. Hai Vectơ Cùng Hướng Khi Nào?
Để xác định khi nào hai vectơ cùng hướng, cần nắm vững khái niệm về giá của vectơ và điều kiện để hai vectơ cùng phương.
2.1. Giá của Vectơ
Giá của một vectơ là đường thẳng đi qua điểm đầu và điểm cuối của vectơ đó.
2.2. Điều Kiện Hai Vectơ Cùng Hướng
Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Hai vectơ được gọi là cùng hướng nếu chúng cùng phương và hướng của chúng trùng nhau. Điều này có nghĩa là, nếu ta vẽ hai vectơ này từ cùng một điểm gốc, chúng sẽ chỉ theo cùng một hướng.
2.3. Ví Dụ Minh Họa
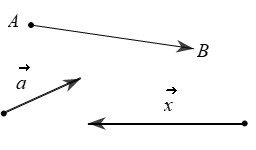
Xét ba vectơ a, b, và c như hình dưới đây:
Trong ví dụ này, vectơ a và vectơ b cùng hướng, vì chúng cùng phương và chỉ theo cùng một hướng. Vectơ c cùng phương với a và b, nhưng ngược hướng với cả hai.
3. Bài Tập Luyện Tập
Để củng cố kiến thức về hai vectơ cùng hướng, hãy cùng giải một số bài tập sau:
Bài 1: Cho lục giác đều ABCDEF tâm O. Hỏi có bao nhiêu vectơ khác vectơ 0 cùng phương với mà điểm đầu và điểm cuối là các đỉnh của lục giác?
A. 4
B. 6
C. 8
D. 10
Hướng dẫn giải:
Bài 2: Mệnh đề nào sau đây là đúng?
A. Hai vectơ cùng phương với vectơ thứ ba khác thì cùng hướng.
B. Hai vectơ cùng phương với vectơ thứ ba khác thì cùng phương.
C. Hai vectơ cùng phương với vectơ thứ ba thì sẽ cùng phương.
D. Hai vectơ ngược hướng với vectơ thứ ba thì cùng hướng.
Hướng dẫn giải:
Đáp án đúng là B. Hai vectơ cùng phương với vectơ thứ ba khác chắc chắn sẽ cùng phương. Các đáp án khác sai do thiếu điều kiện hoặc không chính xác về hướng.
Bài 3: Cho ba điểm phân biệt A, B, C. Khẳng định nào sau đây đúng nhất?
A. A, B, C thẳng hàng khi và chỉ khi và cùng phương.
B. A, B, C thẳng hàng khi và chỉ khi và cùng hướng.
C. A, B, C thẳng hàng khi và chỉ khi và cùng phương.
D. Cả 3 đáp án trên đều đúng.
Hướng dẫn giải:
Đáp án đúng là A. Ba điểm A, B, C thẳng hàng khi và chỉ khi hai vectơ và cùng phương.
Bài 4: Cho điểm A và vectơ a khác vectơ 0. Xác định điểm M sao cho cùng phương với vectơ a.
Hướng dẫn giải:
Điểm M phải nằm trên đường thẳng đi qua A và song song với giá của vectơ a.
Bài 5: Trong hình sau, chỉ ra các vectơ cùng phương, cùng hướng:
Hướng dẫn giải:
- Các vectơ cùng phương:
- Các vectơ cùng hướng:
Bài 6: Cho tứ giác ABCD. Chứng minh tứ giác ABCD là hình bình hành khi và chỉ khi = .
Hướng dẫn giải:
Bài 7: Cho 3 vectơ a, b, c đều khác . Khẳng định “nếu vectơ a và b cùng ngược hướng với vectơ c thì vectơ a và b cùng hướng” là đúng hay sai?
Hướng dẫn giải:
Khẳng định này đúng. Nếu a và b cùng ngược hướng với c, thì a và b phải cùng phương và hướng của chúng ngược với c, do đó a và b cùng hướng.
Hy vọng qua bài viết này, bạn đã nắm vững định nghĩa và điều kiện để hai vectơ cùng hướng. Hãy luyện tập thêm nhiều bài tập để củng cố kiến thức và áp dụng vào giải các bài toán phức tạp hơn.