Trong chương trình Toán lớp 12, bài toán tìm giá trị nhỏ nhất (GTNN) của hàm số là một phần quan trọng và thường xuyên xuất hiện trong các kỳ thi. Để giải quyết dạng toán này một cách hiệu quả, chúng ta cần nắm vững định nghĩa, các phương pháp tìm GTNN trên các miền khác nhau, và các kỹ năng áp dụng linh hoạt.
1. Định Nghĩa Giá Trị Nhỏ Nhất của Hàm Số
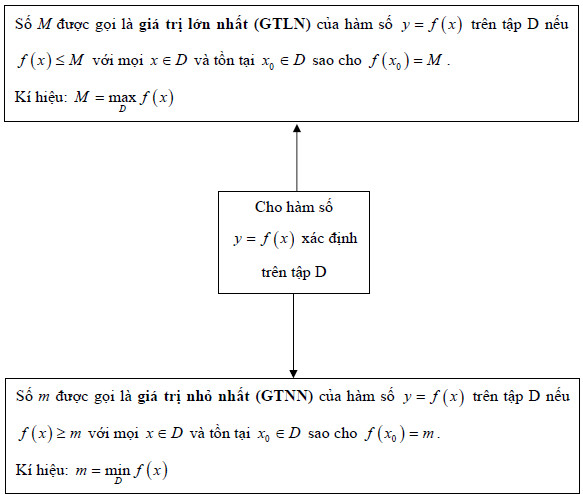
Cho hàm số y = f(x) xác định trên tập D. Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D nếu:
- f(x) ≥ m với mọi x ∈ D
- Tồn tại x₀ ∈ D sao cho f(x₀) = m
Ký hiệu: Min f(x) = m
Sơ đồ trực quan về cách xác định GTNN và GTLN của hàm số, giúp học sinh dễ hình dung và ghi nhớ khái niệm.
2. Phương Pháp Tìm Gtnn Của Hàm Số
Có hai trường hợp chính khi tìm GTNN của hàm số: trên một miền D bất kỳ và trên một đoạn [a; b].
2.1. Tìm GTNN trên Miền D
Khi tìm GTNN của hàm số y = f(x) trên một miền D (có thể là một khoảng, nửa khoảng hoặc toàn bộ tập số thực), ta thường sử dụng phương pháp khảo sát sự biến thiên của hàm số.
- Bước 1: Tìm tập xác định của hàm số.
- Bước 2: Tính đạo hàm f'(x) và tìm các điểm tới hạn (điểm mà tại đó f'(x) = 0 hoặc f'(x) không xác định).
- Bước 3: Lập bảng biến thiên của hàm số. Dựa vào bảng biến thiên để xác định GTNN của hàm số trên D.
Ví dụ minh họa cách tìm GTNN của hàm số bằng phương pháp khảo sát và lập bảng biến thiên, giúp học sinh hiểu rõ từng bước thực hiện.
Ví dụ: Tìm GTNN của hàm số y = x³ – 3x² – 9x + 5.
Giải:
- Tập xác định: D = ℝ.
- y’ = 3x² – 6x – 9. y’ = 0 ⇔ x = -1 hoặc x = 3.
- Lập bảng biến thiên và kết luận: Hàm số đạt GTNN tại x = 3 và Min y = y(3) = -22.
2.2. Tìm GTNN trên Một Đoạn [a; b]
Nếu hàm số f(x) liên tục trên đoạn [a; b], ta có thể áp dụng các bước sau:
- Bước 1: Tính đạo hàm f'(x).
- Bước 2: Tìm các điểm xᵢ ∈ (a; b) mà tại đó f'(xᵢ) = 0 hoặc f'(xᵢ) không xác định.
- Bước 3: Tính các giá trị f(a), f(b), và f(xᵢ).
- Bước 4: So sánh các giá trị trên, giá trị nhỏ nhất trong số đó chính là GTNN của hàm số trên đoạn [a; b].
Ký hiệu: min_[a; b] f(x) = min {f(a); f(b); f(xᵢ)}
Tóm tắt ngắn gọn và dễ hiểu các bước cần thực hiện để tìm GTNN trên một đoạn, giúp học sinh dễ dàng áp dụng vào bài tập.
Ví dụ: Tìm GTNN của hàm số y = (2x + 1) / (x – 2) trên đoạn [-1/2; 1].
Giải:
- y’ = -5 / (x – 2)²
- y’ không xác định tại x = 2, nhưng điểm này không thuộc đoạn [-1/2; 1].
- f(-1/2) = 0; f(1) = -3.
- Vậy min_[-1/2; 1] f(x) = -3.
3. Các Dạng Toán Nâng Cao về GTNN
Ngoài các bài toán cơ bản, còn có các dạng toán phức tạp hơn, đòi hỏi kỹ năng biến đổi và áp dụng linh hoạt các kiến thức.
- Bài toán chứa tham số: Tìm GTNN của hàm số khi có tham số, yêu cầu xác định giá trị của tham số để GTNN đạt giá trị mong muốn.
- Bài toán thực tế: Ứng dụng GTNN để giải quyết các bài toán tối ưu trong thực tế, ví dụ: tìm kích thước hình hộp chữ nhật có thể tích lớn nhất với diện tích toàn phần cho trước.
- Bài toán về hàm số lượng giác: Sử dụng các công thức lượng giác để biến đổi và đưa về dạng đơn giản hơn, sau đó áp dụng các phương pháp tìm GTNN thông thường.
4. Lưu Ý Quan Trọng
- Luôn kiểm tra tập xác định của hàm số trước khi thực hiện các bước giải.
- Cẩn thận khi tính đạo hàm và giải phương trình đạo hàm bằng 0.
- Khi tìm GTNN trên một đoạn, cần so sánh giá trị của hàm số tại các điểm tới hạn và hai đầu đoạn.
- Đối với các bài toán phức tạp, nên thử các phương pháp khác nhau để tìm ra cách giải tối ưu nhất.
Nắm vững lý thuyết và luyện tập thường xuyên là chìa khóa để chinh phục các bài toán tìm GTNN của hàm số. Chúc các bạn học tốt!