Định nghĩa Góc Nội Tiếp
Góc nội tiếp là một khái niệm quan trọng trong hình học phẳng, đặc biệt là khi nghiên cứu về đường tròn. Một góc được gọi là góc nội tiếp nếu thỏa mãn đồng thời hai điều kiện sau:
- Đỉnh của góc nằm trên đường tròn.
- Hai cạnh của góc là hai dây cung của đường tròn đó.
Cung nằm bên trong góc nội tiếp được gọi là cung bị chắn.
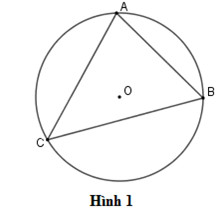Góc nội tiếp chắn cung AB trong đường tròn
Ví dụ: Trên hình vẽ, góc $widehat{ACB}$ là một góc nội tiếp chắn cung AB của đường tròn. Điểm C nằm trên đường tròn, và hai cạnh CA và CB là hai dây cung của đường tròn đó. Cung AB nằm bên trong góc ACB, nên được gọi là cung bị chắn.
Định lý về góc nội tiếp
Định lý quan trọng nhất liên quan đến góc nội tiếp là: Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
Điều này có nghĩa là, nếu góc $widehat{ACB}$ là góc nội tiếp chắn cung AB, thì:
$widehat{ACB} = frac{1}{2} sđ stackrelfrown{AB}$
Ví dụ: Nếu cung AB có số đo là 80 độ, thì góc nội tiếp $widehat{ACB}$ chắn cung AB sẽ có số đo là 40 độ.
Hệ quả của định lý về góc nội tiếp
Định lý về góc nội tiếp kéo theo một số hệ quả quan trọng, thường được sử dụng để giải các bài toán hình học:
a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
Nếu hai góc nội tiếp cùng nằm trong một đường tròn (hoặc hai đường tròn bằng nhau) và có số đo bằng nhau, thì hai cung bị chắn tương ứng cũng có số đo bằng nhau.
b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Nếu hai hoặc nhiều góc nội tiếp cùng chắn một cung, hoặc chắn các cung có số đo bằng nhau, thì các góc đó có số đo bằng nhau. Đây là một hệ quả rất hữu ích để chứng minh các góc bằng nhau trong các bài toán hình học.
c) Góc nội tiếp (nhỏ hơn hoặc bằng 90°) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung.
Góc ở tâm là góc có đỉnh nằm ở tâm của đường tròn. Nếu một góc nội tiếp và một góc ở tâm cùng chắn một cung, thì số đo của góc nội tiếp bằng một nửa số đo của góc ở tâm.
d) Góc nội tiếp chắn nửa đường tròn là góc vuông.
Đây là một trường hợp đặc biệt và rất quan trọng. Nếu góc nội tiếp chắn nửa đường tròn (tức là cung bị chắn là nửa đường tròn), thì góc đó là góc vuông (có số đo bằng 90°). Hệ quả này thường được sử dụng để chứng minh các tam giác vuông hoặc các đường thẳng vuông góc.
Các dạng toán thường gặp về góc nội tiếp
Góc nội tiếp là một chủ đề quan trọng trong chương trình hình học, và có nhiều dạng bài toán khác nhau liên quan đến khái niệm này. Dưới đây là một số dạng toán thường gặp:
Dạng 1: Chứng minh các tam giác đồng dạng, hệ thức về cạnh, hai góc bằng nhau, các đoạn thẳng bằng nhau
Phương pháp giải:
Trong dạng toán này, chúng ta thường sử dụng các hệ quả của định lý về góc nội tiếp để chứng minh các góc bằng nhau. Từ đó, chúng ta có thể sử dụng các tiêu chí đồng dạng của tam giác (ví dụ: góc-góc, cạnh-góc-cạnh, cạnh-cạnh-cạnh) để chứng minh hai tam giác đồng dạng. Khi hai tam giác đồng dạng, chúng ta có thể suy ra các hệ thức về cạnh hoặc các đoạn thẳng bằng nhau.
Dạng 2: Chứng minh hai đường thẳng vuông góc, song song. Tính độ dài, diện tích
Phương pháp giải:
Trong dạng toán này, chúng ta thường sử dụng hệ quả về góc nội tiếp chắn nửa đường tròn là góc vuông để chứng minh hai đường thẳng vuông góc. Hoặc, chúng ta có thể sử dụng các hệ quả khác để suy ra các góc bằng nhau, từ đó chứng minh hai đường thẳng song song (ví dụ: hai góc so le trong bằng nhau, hai góc đồng vị bằng nhau). Sau khi đã chứng minh được các quan hệ vuông góc hoặc song song, chúng ta có thể sử dụng các kiến thức về hình học và lượng giác để tính độ dài các đoạn thẳng hoặc diện tích các hình.