Góc nội tiếp là một khái niệm quan trọng trong hình học phẳng, đặc biệt khi nghiên cứu về đường tròn. Một trường hợp đặc biệt và hữu ích là góc nội tiếp chắn nửa đường tròn. Bài viết này sẽ đi sâu vào tính chất này, các ứng dụng của nó và cách giải các bài toán liên quan.
Định Nghĩa Góc Nội Tiếp
Góc nội tiếp là một góc có đỉnh nằm trên đường tròn và hai cạnh của góc là hai dây cung của đường tròn đó. Cung nằm bên trong góc được gọi là cung bị chắn.
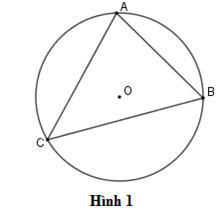Góc nội tiếp chắn cung AB
Định lý: Góc nội tiếp đỉnh C trên đường tròn chắn cung AB.
Định Lý Cơ Bản về Góc Nội Tiếp
Số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn. Ví dụ, nếu góc nội tiếp (widehat{ACB}) chắn cung AB, thì (widehat{ACB} = frac{1}{2} sđ stackrelfrown{AB}).
Hệ Quả Quan Trọng của Góc Nội Tiếp
Trong một đường tròn:
- Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
- Các góc nội tiếp cùng chắn một cung thì bằng nhau.
- Góc nội tiếp (nhỏ hơn hoặc bằng 90°) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung.
- Góc Nội Tiếp Chắn Nửa đường Tròn Là Góc vuông. Đây là hệ quả quan trọng nhất mà chúng ta sẽ tập trung vào.
Góc Nội Tiếp Chắn Nửa Đường Tròn Là Góc Vuông
Hệ quả này nói rằng nếu một góc nội tiếp chắn nửa đường tròn, thì góc đó là góc vuông (90°). Điều này có nghĩa là nếu ta có một đường tròn và một đường kính AB, bất kỳ điểm C nào nằm trên đường tròn (không trùng với A hoặc B) sẽ tạo thành một góc ACB là góc vuông.
Ứng Dụng Của Góc Nội Tiếp Chắn Nửa Đường Tròn
- Chứng minh tam giác vuông: Nếu bạn có một tam giác nội tiếp đường tròn và một cạnh của tam giác là đường kính của đường tròn, thì tam giác đó là tam giác vuông.
- Tìm tâm đường tròn ngoại tiếp tam giác vuông: Tâm của đường tròn ngoại tiếp một tam giác vuông nằm ở trung điểm của cạnh huyền.
- Giải các bài toán hình học phức tạp: Tính chất này giúp đơn giản hóa nhiều bài toán, đặc biệt là khi liên quan đến các góc và đường tròn.
Các Dạng Toán Thường Gặp và Phương Pháp Giải
Dạng 1: Chứng minh các tam giác đồng dạng, hệ thức về cạnh, hai góc bằng nhau, các đoạn thẳng bằng nhau.
Phương pháp: Sử dụng các hệ quả của góc nội tiếp, đặc biệt là tính chất “Các góc nội tiếp cùng chắn một cung thì bằng nhau” và “Góc nội tiếp chắn nửa đường tròn là góc vuông”.
Dạng 2: Chứng minh hai đường thẳng vuông góc, song song. Tính độ dài, diện tích.
Phương pháp: Sử dụng hệ quả về góc nội tiếp để suy ra các góc bằng nhau, từ đó chứng minh theo yêu cầu bài toán. Ví dụ, nếu bạn chứng minh được một góc nội tiếp chắn nửa đường tròn, bạn có thể suy ra hai đường thẳng tạo nên góc đó vuông góc với nhau.
