Bài toán xác định góc giữa đường thẳng và mặt phẳng là một dạng toán quan trọng trong chương trình hình học không gian lớp 11. Bài viết này sẽ trình bày chi tiết cách giải bài toán tìm “Góc Giữa Sb Và Sac” trong một hình chóp cụ thể.
Đề bài: Cho hình chóp S.ABC có SA vuông góc với đáy, tam giác ABC vuông tại B. Biết SA = AB = BC. Tính góc giữa đường thẳng SB và mặt phẳng (SAC).
Lời giải:
Để giải bài toán này, ta cần xác định hình chiếu vuông góc của đường thẳng SB lên mặt phẳng (SAC). Từ đó, góc giữa SB và (SAC) chính là góc giữa SB và hình chiếu đó.
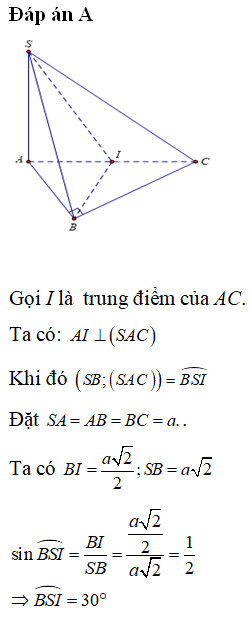Hình chóp S.ABC với SA vuông góc với đáy, tam giác ABC vuông tại B, tính góc giữa SB và mặt phẳng SAC
Phân tích hình vẽ và các yếu tố đã cho:
- SA vuông góc với mặt phẳng đáy (ABC), nghĩa là SA vuông góc với mọi đường thẳng nằm trong mặt phẳng (ABC), đặc biệt là AB và AC.
- Tam giác ABC vuông tại B, nghĩa là AB vuông góc với BC.
- SA = AB = BC. Đây là một dữ kiện quan trọng giúp ta xác định các tỉ lệ và tính toán độ dài các đoạn thẳng.
Để tìm hình chiếu của SB lên (SAC), ta làm như sau:
-
Xác định giao điểm: Giao điểm của SB và (SAC) là điểm S.
-
Tìm hình chiếu của B lên (SAC): Vì SA vuông góc với (ABC) nên mặt phẳng (SAC) cũng vuông góc với (ABC). Do đó, hình chiếu của B lên (SAC) sẽ là giao điểm của đường thẳng vuông góc với (SAC) kẻ từ B với mặt phẳng (SAC). Gọi H là hình chiếu của B lên AC. Do tam giác ABC vuông tại B, ta có BH vuông góc với AC. Vì SA vuông góc với đáy nên SA vuông góc với BH. Vậy BH vuông góc với (SAC). Suy ra, hình chiếu của B trên (SAC) là H.
-
Kết luận: Hình chiếu của SB lên (SAC) là SH. Vậy, góc giữa SB và (SAC) là góc BSH.
Bây giờ, ta cần tính góc BSH. Xét tam giác vuông ABH, ta có:
- AB = SA (theo giả thiết)
- BC = AB (theo giả thiết)
Vì BH vuông góc với (SAC), nên tam giác SHB vuông tại H. Ta có:
tan(BSH) = BH / SH
Để tính BH và SH, ta cần thêm một vài bước:
- Tính AC: Vì tam giác ABC vuông tại B và AB = BC, nên AC = AB√2 = SA√2.
- Tính BH: Trong tam giác vuông ABC, BH là đường cao ứng với cạnh huyền AC. Ta có BH = (AB BC) / AC = (SA SA) / (SA√2) = SA / √2.
- Tính SH: Áp dụng định lý Pythagoras cho tam giác vuông SAH (vuông tại A), ta có SH = √(SA² + AH²). Để tính AH, ta có AH = AC – HC. Vì BH là đường cao trong tam giác vuông ABC, ta có HC = BC²/AC = SA² / (SA√2) = SA/√2. Do đó, AH = SA√2 – SA/√2 = SA/√2. Vậy SH = √(SA² + (SA/√2)²) = √(SA² + SA²/2) = SA√(3/2).
Vậy, tan(BSH) = (SA/√2) / (SA√(3/2)) = 1/√3. Suy ra, góc BSH = 30 độ.
Kết luận: Góc giữa đường thẳng SB và mặt phẳng (SAC) là 30 độ.
