Góc Có Cạnh Tương ứng Vuông Góc là một khái niệm quan trọng trong hình học, đặc biệt khi nghiên cứu về các mối quan hệ giữa các đường thẳng và góc. Chúng ta sẽ khám phá tính chất cơ bản và cách chứng minh các định lý liên quan đến loại góc này.
Định nghĩa: Hai góc được gọi là có cạnh tương ứng vuông góc nếu mỗi cạnh của góc này vuông góc với một cạnh của góc kia.
Định lý 1: Hai góc có cạnh tương ứng vuông góc thì bằng nhau hoặc bù nhau.
Để chứng minh định lý này, ta xét hai trường hợp:
Trường hợp 1: Các góc nhọn hoặc tù.
Chứng minh:
Vẽ (O’m//Ox) và (O’n//Oy). Cách vẽ này giúp chúng ta tạo ra các góc song song và vuông góc để dễ dàng so sánh.
Vì (left{ begin{array}{l}O’x’ bot Ox\O’m//Oxend{array} right.) nên (O’x’ bot O’m). Điều này suy ra (angle mO’x’ = 90^circ left( 1 right)).
Tương tự, vì (left{ begin{array}{l}O’y’ bot Oy\O’n//Oyend{array} right.) nên (O’y’ bot O’n), dẫn đến (angle nO’y’ = 90^circ left( 2 right)).
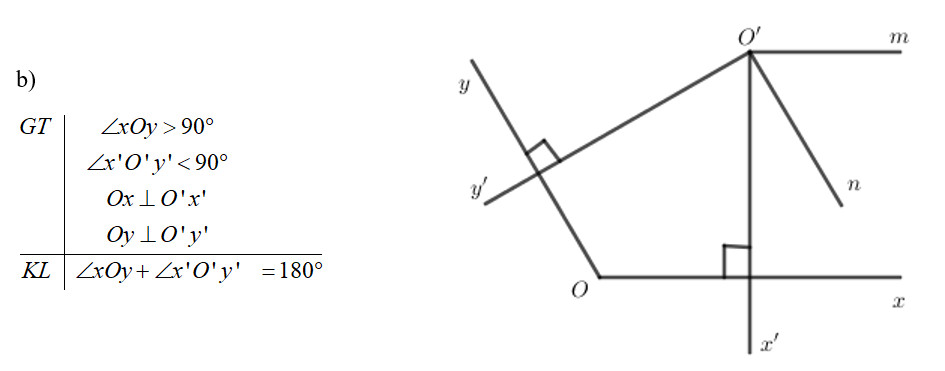Hai góc xOy và x'O'y' có cạnh tương ứng vuông góc và bằng nhau.
Hình ảnh minh họa hai góc xOy và x’O’y’ có cạnh tương ứng vuông góc và bằng nhau, sử dụng các đường thẳng song song và vuông góc để chứng minh tính chất.
Ta có: (left{ begin{array}{l}angle mO’x’ = angle mOn + angle nO’x’ = 90^circ \angle nO’y’ = angle x’O’y’ + angle nO’x’ = 90^circ end{array} right.)
Suy ra (angle x’O’y’ = angle mOn) (cùng phụ với góc (angle nO’x’)).
Vì (left{ begin{array}{l}O’n//Oy\O’m//Oxend{array} right.) nên theo kết quả của bài 9, ta có: (angle xOy = angle mOn). Mà (angle x’O’y’ = angle mOn)
Suy ra (angle xOy = angle x’O’y’left( { = angle mOn} right)) (đpcm). Vậy hai góc này bằng nhau.
Trường hợp 2: Hai góc bù nhau.
Chứng minh tương tự, nhưng ta có:
Vì (left{ begin{array}{l}O’n//Oy\O’m//Oxend{array} right.) nên theo kết quả của bài 9, ta có: (angle xOy + angle mOn = 180^circ ). Mà (angle x’O’y’ = angle mOn)
Suy ra (angle xOy + angle x’O’y’ = 180^circ ) (đpcm). Do đó hai góc này bù nhau.
Định lý 2: Nếu hai cạnh của một góc vuông góc với hai cạnh của một góc khác thì hai góc đó bằng nhau.
Chứng minh:
Vì (left. begin{array}{l}Oy bot Ox\O’x’ bot Oxend{array} right} Rightarrow Oy//O’x’)
Vì (left. begin{array}{l}Oy//O’x’\Oy bot O’y’end{{array} right} Rightarrow O’x’ bot O’y’)
( Rightarrow angle x’O’y’ = 90^circ ) (đpcm)
Ứng dụng:
Tính chất về góc có cạnh tương ứng vuông góc được sử dụng rộng rãi trong việc giải các bài toán hình học, đặc biệt là trong các bài toán liên quan đến tam giác, đường tròn và các hình đa giác khác. Việc nắm vững tính chất này giúp chúng ta dễ dàng suy luận và chứng minh các định lý phức tạp hơn.
Ví dụ, trong thiết kế kỹ thuật, kiến trúc, và xây dựng, việc hiểu rõ và áp dụng chính xác các tính chất của góc có cạnh tương ứng vuông góc là rất quan trọng để đảm bảo tính chính xác và an toàn của công trình.
