Trong hình học, một trong những khái niệm quan trọng và thú vị là giao điểm của ba đường phân giác trong tam giác. Vậy, Giao điểm 3 đường Phân Giác Gọi Là Gì? Câu trả lời chính xác là tâm đường tròn nội tiếp tam giác. Để hiểu rõ hơn về khái niệm này, chúng ta sẽ đi sâu vào định nghĩa, tính chất và ứng dụng của nó.
Định Nghĩa Tâm Đường Tròn Nội Tiếp
Tâm đường tròn nội tiếp của một tam giác là điểm đồng quy của ba đường phân giác trong của tam giác đó. Điểm này cũng là tâm của đường tròn duy nhất tiếp xúc với cả ba cạnh của tam giác.
Tính Chất Quan Trọng Của Tâm Đường Tròn Nội Tiếp
Tâm đường tròn nội tiếp có một tính chất vô cùng quan trọng:
- Cách đều ba cạnh của tam giác: Khoảng cách từ tâm đường tròn nội tiếp đến mỗi cạnh của tam giác là bằng nhau và bằng bán kính của đường tròn nội tiếp.
Tính chất này giúp ta xác định được vị trí chính xác của tâm đường tròn nội tiếp và là cơ sở để giải nhiều bài toán liên quan.
Minh Họa Bằng Hình Ảnh
Để dễ hình dung, hãy xem hình ảnh sau:
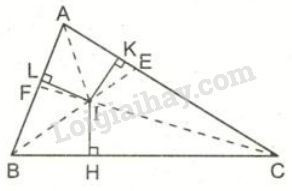Tam giác ABC với đường tròn nội tiếp và tâm I, các đường phân giác cắt nhau tại I
Trong hình, điểm I là tâm đường tròn nội tiếp tam giác ABC. Ba đường phân giác của các góc A, B, và C cắt nhau tại I. Đường tròn tâm I tiếp xúc với cả ba cạnh của tam giác.
Ứng Dụng Của Tâm Đường Tròn Nội Tiếp
Tâm đường tròn nội tiếp không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tế trong các bài toán hình học và các lĩnh vực liên quan. Dưới đây là một vài ví dụ:
- Giải các bài toán chứng minh: Sử dụng tính chất cách đều ba cạnh để chứng minh các đoạn thẳng bằng nhau, các đường thẳng song song hoặc vuông góc.
- Tìm quỹ tích điểm: Xác định tập hợp các điểm thỏa mãn một điều kiện nào đó liên quan đến khoảng cách đến các cạnh của tam giác.
- Ứng dụng trong thiết kế: Trong kiến trúc và kỹ thuật, việc xác định tâm đường tròn nội tiếp có thể giúp thiết kế các cấu trúc hài hòa và cân đối.
Mở Rộng Kiến Thức Về Đường Phân Giác
Ngoài việc tìm hiểu về giao điểm của ba đường phân giác, chúng ta cũng nên nắm vững các kiến thức cơ bản về đường phân giác trong tam giác:
- Định nghĩa: Đường phân giác của một góc là đường thẳng chia góc đó thành hai góc bằng nhau.
- Tính chất: Điểm nằm trên đường phân giác của một góc thì cách đều hai cạnh của góc đó.
- Đường phân giác trong và ngoài: Mỗi góc của tam giác có một đường phân giác trong và một đường phân giác ngoài. Đường phân giác trong chia góc thành hai góc bằng nhau, còn đường phân giác ngoài chia góc ngoài thành hai góc bằng nhau.
Hiểu rõ các khái niệm và tính chất này sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và hiệu quả hơn.
Tóm lại, giao điểm 3 đường phân giác gọi là tâm đường tròn nội tiếp tam giác. Đây là một khái niệm quan trọng với nhiều ứng dụng trong hình học và thực tiễn. Việc nắm vững định nghĩa, tính chất và các kiến thức liên quan sẽ giúp bạn nâng cao khả năng giải toán và ứng dụng vào các lĩnh vực khác.
