Trong cơ học kết cấu, việc xác định phản lực liên kết là một bước quan trọng để phân tích và thiết kế các công trình. Bài viết này sẽ hướng dẫn bạn cách xác định và tính toán phản lực liên kết một cách chi tiết và dễ hiểu.
1. Khái Niệm Cơ Bản về Lực, Moment và Cơ Hệ
Trước khi đi vào Giải Bài Tập Xác định Phản Lực Liên Kết, chúng ta cần nắm vững các khái niệm cơ bản sau:
-
Lực: Là đại lượng vectơ biểu thị tác dụng cơ học giữa các vật, có thể làm thay đổi trạng thái chuyển động hoặc gây biến dạng. Lực được đặc trưng bởi điểm đặt, phương, chiều và độ lớn (đơn vị Newton – N).
-
Moment (Mô men): Thể hiện tác động làm quay vật thể quanh một điểm hoặc trục. Moment được tính bằng tích của lực và khoảng cách từ điểm đặt lực đến tâm quay (cánh tay đòn). Đơn vị của moment là N.m.
-
Cơ Hệ: Là tập hợp các chất điểm hoặc vật thể có liên quan về mặt cơ học.
-
Hệ Lực: Tập hợp các lực tác dụng lên một cơ hệ.
-
Hệ Lực Cân Bằng: Hệ lực có tổng hợp lực và tổng moment bằng không. Hệ lực cân bằng không gây ra bất kỳ tác dụng cơ học nào lên cơ hệ.
2. Các Loại Liên Kết và Phản Lực Liên Kết Thường Gặp
Liên kết là các ràng buộc hạn chế chuyển động của vật thể. Mỗi loại liên kết sẽ sinh ra các phản lực liên kết tương ứng, chống lại các chuyển động bị hạn chế. Dưới đây là các loại liên kết phổ biến:
-
Liên Kết Cố Định (Gối Cố Định): Hạn chế chuyển động theo cả phương ngang và phương thẳng đứng. Tại gối cố định, sẽ xuất hiện hai phản lực liên kết: một theo phương ngang (H) và một theo phương thẳng đứng (V).
-
Gối Di Động: Hạn chế chuyển động theo phương vuông góc với mặt trượt. Tại gối di động, chỉ có một phản lực liên kết theo phương vuông góc với phương trượt (V).
-
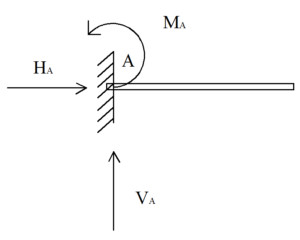
Liên Kết Ngàm (Liên Kết Cứng): Hạn chế cả chuyển động tịnh tiến và chuyển động quay. Tại liên kết ngàm, sẽ xuất hiện hai phản lực liên kết (H và V) và một moment phản lực (M).
3. Các Bước Giải Bài Tập Xác Định Phản Lực Liên Kết
Để giải bài tập xác định phản lực liên kết, chúng ta thực hiện theo các bước sau:
-
Bước 1: Xác định và Ký Hiệu Phản Lực Liên Kết (PLLK) lên hình vẽ. Xác định loại liên kết tại mỗi điểm và vẽ các phản lực liên kết tương ứng. Lưu ý chọn chiều của các phản lực một cách tùy ý. Nếu kết quả tính toán là âm, điều đó có nghĩa là chiều thực tế của phản lực ngược với chiều đã chọn.
-
Bước 2: Phân Loại Lực Tác Dụng. Chia các lực tác dụng lên cơ hệ thành hai loại: lực hoạt động (ngoại lực tác dụng trực tiếp lên cơ hệ) và phản lực liên kết.
-
Bước 3: Thiết Lập Phương Trình Cân Bằng. Áp dụng các phương trình cân bằng tĩnh học để thiết lập hệ phương trình. Các phương trình cân bằng bao gồm:
- Tổng các lực theo phương ngang bằng 0: ΣFx = 0
- Tổng các lực theo phương thẳng đứng bằng 0: ΣFy = 0
- Tổng các moment đối với một điểm bất kỳ bằng 0: ΣM = 0
-
Bước 4: Giải Hệ Phương Trình và Kết Luận. Giải hệ phương trình để tìm ra các phản lực liên kết. Dựa vào dấu của kết quả để xác định chiều thực tế của các phản lực.
4. Ví Dụ Minh Họa
Ví dụ 1: Cho cơ hệ cân bằng như hình vẽ. Cho biết: M = 20 kN.m, lực phân bố đều q = 1 kN/m, P = 0,6 kN, AB = CD = a = 0,6m, AC = b = 2m. Xác định phản lực liên kết tại A và C.
Giải:
-
Xác định và ký hiệu phản lực liên kết: Tại A là gối cố định, có 2 phản lực là XA và YA. Tại C là gối di động, có 1 phản lực là YC.
-
Phân loại lực: Lực phân bố đều q, lực tập trung P, moment M và các phản lực liên kết XA, YA, YC.
-
Thiết lập phương trình cân bằng:
- ΣFx = 0: XA = 0
- ΣFy = 0: YA + YC – q(a+b+a) – P = 0
- ΣMA = 0: -M + YC(b+a+a) – q(a+b+a)(a+b/2+a/2) – P(a+b) = 0
-
Giải hệ phương trình: Từ hệ phương trình trên, ta tìm được XA = 0, YA và YC.
-
Kết luận: Sau khi giải hệ phương trình, ta sẽ có giá trị cụ thể của các phản lực liên kết tại A và C.
Ví dụ 2: Cho cơ hệ cân bằng như hình vẽ. Cho biết: P = 100N, q = 20N/m, AD = BD = 1m, BC = 2m, M = 50 Nm. Xác định phản lực liên kết tại A, C và lực liên kết tại B.
Giải:
-
Xác định và ký hiệu phản lực liên kết: Tương tự như ví dụ 1, xác định các phản lực tại A, C và lực liên kết tại B.
-
Phân loại lực: Lực P, lực phân bố q, moment M và các phản lực liên kết.
-
Thiết lập phương trình cân bằng: Lưu ý chọn hệ tọa độ phù hợp và quy ước dấu cho moment.
-
Giải hệ phương trình: Giải hệ phương trình để tìm các phản lực liên kết.
-
Kết luận: Dựa vào kết quả để xác định chiều và độ lớn của các phản lực liên kết.
Hy vọng với hướng dẫn chi tiết này, bạn có thể dễ dàng giải các bài tập xác định phản lực liên kết trong cơ học kết cấu. Chúc bạn thành công!