Tìm Giá Trị Nhỏ Nhất Của Biểu Thức f(x, y) = x – 2y: Phương Pháp và Ví Dụ Chi Tiết

Để tìm giá trị nhỏ nhất của biểu thức f(x, y) = x - 2y trong một miền nghiệm xác định, chúng ta thường sử dụng phương pháp hình học kết hợp với đại số. Bài viết này sẽ trình bày chi tiết phương pháp này thông qua một ví dụ cụ thể.

Giả sử chúng ta có một hệ bất phương trình xác định một miền nghiệm trên mặt phẳng tọa độ. Mục tiêu là tìm điểm (x, y) trong miền nghiệm này sao cho biểu thức f(x, y) = x - 2y đạt giá trị nhỏ nhất.

Bước 1: Xác định Miền Nghiệm

Miền nghiệm là tập hợp tất cả các điểm (x, y) thỏa mãn đồng thời tất cả các bất phương trình trong hệ. Để xác định miền nghiệm, ta thực hiện các bước sau:

1. Vẽ các đường thẳng: Vẽ các đường thẳng tương ứng với mỗi bất phương trình bằng cách thay dấu bất đẳng thức bằng dấu bằng.
2. Xác định nửa mặt phẳng: Với mỗi đường thẳng, xác định nửa mặt phẳng thỏa mãn bất phương trình tương ứng. Có thể sử dụng một điểm thử (ví dụ: gốc tọa độ O(0; 0)) để kiểm tra. Nếu điểm thử thỏa mãn bất phương trình, thì nửa mặt phẳng chứa điểm thử là miền nghiệm của bất phương trình đó.
3. Tìm giao của các miền: Miền nghiệm của hệ bất phương trình là giao của tất cả các nửa mặt phẳng đã xác định.

Ví dụ, xét hệ bất phương trình sau:

• 0 ≤ y ≤ 5
• x ≥ 0
• x + y - 2 ≥ 0
• x - y - 2 ≤ 0

Chúng ta sẽ vẽ các đường thẳng x + y - 2 = 0, x - y - 2 = 0, y = 5, x = 0 và y = 0, sau đó xác định miền nghiệm dựa trên các điều kiện đã cho.

Bước 2: Xác định Các Điểm Góc (Vertices)

Miền nghiệm thường là một đa giác (hoặc một miền không giới hạn). Các điểm góc (vertices) của đa giác này là giao điểm của các đường thẳng biên. Chúng ta cần xác định tọa độ của tất cả các điểm góc này.

Ví dụ, dựa trên miền nghiệm được xác định bởi hệ bất phương trình trên, chúng ta có thể xác định các điểm góc là A(7; 5), B(0; 5), C(0; 2), và D(2; 0).

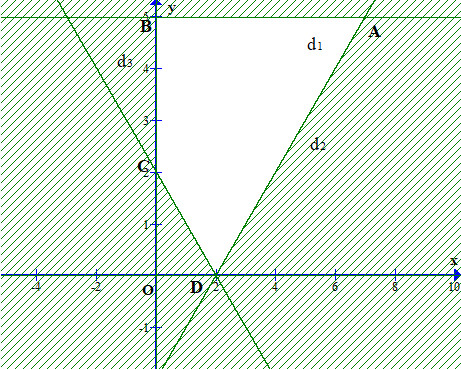Miền nghiệm của hệ bất phương trình và các điểm góc A, B, C, D.

Bước 3: Tính Giá Trị Của Biểu Thức Tại Các Điểm Góc

Tính giá trị của biểu thức f(x, y) = x - 2y tại mỗi điểm góc đã xác định ở bước 2.

Trong ví dụ trên, ta có:

• f(7; 5) = 7 - 2 * 5 = -3
• f(0; 5) = 0 - 2 * 5 = -10
• f(0; 2) = 0 - 2 * 2 = -4
• f(2; 0) = 2 - 2 * 0 = 2

Bước 4: Xác Định Giá Trị Nhỏ Nhất

So sánh các giá trị đã tính ở bước 3. Giá trị nhỏ nhất trong số đó chính là giá trị nhỏ nhất của biểu thức f(x, y) trên miền nghiệm đã cho.

Trong ví dụ trên, giá trị nhỏ nhất là -10, đạt được tại điểm B(0; 5).

Kết luận

Giá trị nhỏ nhất của biểu thức f(x, y) = x - 2y trong miền nghiệm xác định bởi hệ bất phương trình 0 ≤ y ≤ 5, x ≥ 0, x + y - 2 ≥ 0, và x - y - 2 ≤ 0 là -10.

Phương pháp này có thể áp dụng cho nhiều bài toán tìm giá trị lớn nhất hoặc nhỏ nhất của một biểu thức tuyến tính trên một miền nghiệm được xác định bởi một hệ bất phương trình tuyến tính. Quan trọng là xác định chính xác miền nghiệm và các điểm góc của nó.