Chuyển động tròn đều là một dạng chuyển động đặc biệt, thường gặp trong thực tế và có nhiều ứng dụng quan trọng. Một trong những yếu tố then chốt để mô tả chuyển động này chính là gia tốc, đặc biệt là gia tốc hướng tâm. Bài viết này sẽ đi sâu vào khái niệm, công thức tính, và các ví dụ minh họa về Gia Tốc Của Chuyển động Tròn đều.
1. Chuyển Động Tròn Đều và Gia Tốc Hướng Tâm
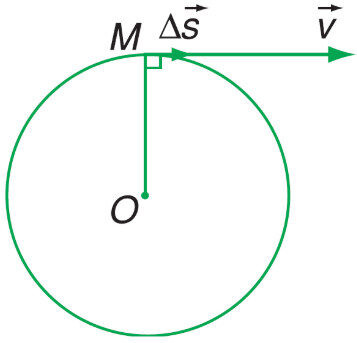
Chuyển động tròn đều là chuyển động mà vật di chuyển trên một quỹ đạo tròn với tốc độ không đổi. Mặc dù tốc độ không đổi, vận tốc lại liên tục thay đổi về hướng. Sự thay đổi vận tốc này tạo ra gia tốc, và trong chuyển động tròn đều, gia tốc này luôn hướng về tâm của đường tròn, do đó được gọi là gia tốc hướng tâm.
Hình ảnh minh họa vectơ gia tốc hướng tâm luôn hướng về tâm quỹ đạo, biểu diễn sự thay đổi hướng vận tốc trong chuyển động tròn đều.
Các đặc điểm quan trọng của chuyển động tròn đều cần nắm vững:
- Quỹ đạo: Hình tròn.
- Tốc độ dài: Không đổi.
- Tốc độ góc: Không đổi.
Hình ảnh mô tả vectơ vận tốc luôn tiếp tuyến với đường tròn quỹ đạo và liên tục thay đổi hướng.
2. Công Thức Tính Gia Tốc Hướng Tâm
Gia tốc của chuyển động tròn đều, hay gia tốc hướng tâm, được tính theo các công thức sau:
aht = v²/r = rω²
Trong đó:
ahtlà gia tốc hướng tâm (m/s²)vlà tốc độ dài (m/s)ωlà tốc độ góc (rad/s)rlà bán kính quỹ đạo (m)
Tốc độ góc ω liên hệ với chu kỳ T (thời gian vật đi hết một vòng) và tần số f (số vòng vật đi được trong một giây) theo các công thức:
ω = 2π/T = 2πf
3. Ví Dụ Minh Họa
Để hiểu rõ hơn về gia tốc của chuyển động tròn đều, hãy xem xét ví dụ sau:
Ví dụ: Một chiếc xe đua chạy trên đường đua hình tròn có bán kính 500m với tốc độ 180 km/h. Tính gia tốc hướng tâm của xe.
Giải:
- Đổi tốc độ: 180 km/h = 50 m/s
- Áp dụng công thức: aht = v²/r = (50 m/s)² / 500 m = 5 m/s²
Vậy, gia tốc hướng tâm của xe đua là 5 m/s².
Hình ảnh minh họa chuyển động tròn đều của Mặt Trăng quanh Trái Đất, một ví dụ điển hình về gia tốc hướng tâm.
4. Bài Tập Vận Dụng
Để củng cố kiến thức về gia tốc của chuyển động tròn đều, hãy thử sức với các bài tập sau:
Bài 1: Một em bé ngồi trên đu quay, cách tâm đu quay 3m. Đu quay quay một vòng hết 6 giây. Tính gia tốc hướng tâm của em bé.
Bài 2: Một vệ tinh nhân tạo bay quanh Trái Đất ở độ cao 300 km so với bề mặt Trái Đất. Biết bán kính Trái Đất là 6400 km và chu kỳ quay của vệ tinh là 90 phút. Tính gia tốc hướng tâm của vệ tinh.
Bài 3: Một chiếc xe máy chuyển động đều trên một đường tròn có bán kính 80m. Biết tốc độ dài của xe là 36km/h. Tính gia tốc hướng tâm của xe.
5. Ứng Dụng Thực Tế
Gia tốc của chuyển động tròn đều có nhiều ứng dụng quan trọng trong khoa học và kỹ thuật, ví dụ:
- Thiết kế đường đua: Các kỹ sư sử dụng kiến thức về gia tốc hướng tâm để thiết kế các khúc cua trên đường đua, đảm bảo an toàn cho các phương tiện di chuyển với tốc độ cao.
- Vệ tinh nhân tạo: Việc tính toán gia tốc hướng tâm giúp xác định quỹ đạo và duy trì vị trí của vệ tinh quanh Trái Đất.
- Máy ly tâm: Ứng dụng gia tốc hướng tâm để tách các thành phần của hỗn hợp, ví dụ như tách máu thành huyết tương và tế bào máu.
6. Tổng Kết
Gia tốc của chuyển động tròn đều là một khái niệm quan trọng trong vật lý. Nắm vững định nghĩa, công thức tính và các ví dụ minh họa sẽ giúp bạn hiểu rõ hơn về chuyển động này và ứng dụng nó vào giải quyết các bài toán thực tế. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về gia tốc hướng tâm.