Tam thức bậc hai đóng vai trò quan trọng trong toán học phổ thông và có nhiều ứng dụng thực tế. Một câu hỏi thường gặp là khi nào thì tam thức bậc hai $f(x) ge 0$ với mọi $x$ thuộc tập số thực $R$? Bài viết này sẽ đi sâu vào vấn đề này, cung cấp kiến thức đầy đủ và các ví dụ minh họa.
1. Tam thức bậc hai và điều kiện $f(x) ge 0$ với mọi x
Tam thức bậc hai có dạng tổng quát: $f(x) = ax^2 + bx + c$, trong đó $a, b, c$ là các hệ số và $a ne 0$.
Để $f(x) ge 0$ với mọi $x in R$, điều kiện cần và đủ là:
- $a > 0$ (parabol hướng lên trên)
- $Delta le 0$, trong đó $Delta = b^2 – 4ac$ là delta của tam thức bậc hai (để đồ thị không cắt hoặc chỉ tiếp xúc với trục hoành).
Hình ảnh minh họa parabol có hệ số a dương và delta nhỏ hơn hoặc bằng 0, thể hiện f(x) luôn lớn hơn hoặc bằng 0.
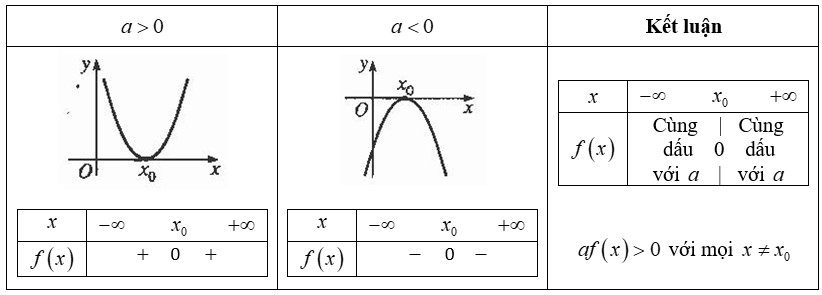
2. Định lý về dấu của tam thức bậc hai và mối liên hệ với $f(x) ge 0$
Định lý về dấu của tam thức bậc hai cho biết:
-
Nếu $Delta < 0$: $f(x)$ cùng dấu với $a$ với mọi $x in R$. Vậy, để $f(x) ge 0$ thì $a > 0$.
-
Nếu $Delta = 0$: $f(x)$ cùng dấu với $a$ với mọi $x ne -frac{b}{2a}$. Vậy, để $f(x) ge 0$ thì $a > 0$ và $f(-frac{b}{2a}) = 0$.
-
Nếu $Delta > 0$: $f(x)$ có hai nghiệm phân biệt $x_1$ và $x_2$. $f(x)$ cùng dấu với $a$ khi $x < x_1$ hoặc $x > x_2$, và trái dấu với $a$ khi $x_1 < x < x_2$. Trường hợp này không thỏa mãn $f(x) ge 0$ với mọi $x in R$.
3. Minh họa hình học và ý nghĩa của điều kiện
Về mặt hình học, điều kiện $f(x) ge 0$ với mọi $x in R$ có nghĩa là đồ thị của hàm số $y = f(x)$ (là một parabol) phải nằm hoàn toàn phía trên hoặc tiếp xúc với trục hoành. Điều này chỉ xảy ra khi parabol quay lên trên ($a > 0$) và không cắt trục hoành ($Delta le 0$).
Hình ảnh minh họa các trường hợp đồ thị của tam thức bậc hai, tập trung vào các trường hợp delta âm và delta bằng 0 để làm nổi bật điều kiện f(x) >= 0.
4. Ứng dụng của điều kiện $f(x) ge 0$ trong giải toán
Điều kiện $f(x) ge 0$ với mọi $x in R$ được sử dụng rộng rãi trong giải các bài toán sau:
- Tìm điều kiện để bất phương trình bậc hai nghiệm đúng với mọi x: Ví dụ, tìm $m$ để $x^2 + 2mx + m + 2 > 0$ với mọi $x$. Ta cần có $Delta’ = m^2 – (m + 2) < 0$.
- Xét tính xác định của hàm số: Ví dụ, hàm số $y = sqrt{ax^2 + bx + c}$ xác định trên $R$ khi và chỉ khi $ax^2 + bx + c ge 0$ với mọi $x$.
- Chứng minh bất đẳng thức: Đôi khi, việc chứng minh một bất đẳng thức có thể quy về việc chứng minh một tam thức bậc hai luôn không âm.
5. Ví dụ minh họa
Ví dụ 1: Tìm $m$ để $f(x) = x^2 – 2(m+1)x + m^2 + 3 > 0$ với mọi $x in R$.
Giải:
Để $f(x) > 0$ với mọi $x$, ta cần:
- $a = 1 > 0$ (luôn đúng)
- $Delta’ = (m+1)^2 – (m^2 + 3) < 0$
- $m^2 + 2m + 1 – m^2 – 3 < 0$
- $2m – 2 < 0$
- $m < 1$
Vậy, $m < 1$ là điều kiện cần tìm.
Hình ảnh minh họa cách giải một bài toán cụ thể, áp dụng điều kiện delta nhỏ hơn 0 để tìm giá trị của tham số m khi f(x) > 0.
Ví dụ 2: Tìm $m$ để phương trình $(m-1)x^2 + 2(m-1)x + m + 3 = 0$ vô nghiệm.
Giải:
Để phương trình vô nghiệm, xét hai trường hợp:
- Trường hợp 1: $m – 1 = 0 Leftrightarrow m = 1$. Khi đó phương trình trở thành $0x^2 + 0x + 4 = 0$, vô nghiệm. Vậy $m = 1$ thỏa mãn.
- Trường hợp 2: $m – 1 ne 0 Leftrightarrow m ne 1$. Khi đó phương trình là phương trình bậc hai. Để phương trình vô nghiệm, ta cần $Delta’ < 0$.
- $Delta’ = (m-1)^2 – (m-1)(m+3) < 0$
- $(m-1)(m-1 – m – 3) < 0$
- $(m-1)(-4) < 0$
- $m – 1 > 0$
- $m > 1$
Kết hợp cả hai trường hợp, ta có $m ge 1$.
Hình ảnh minh họa cách xét các trường hợp của tham số m để phương trình bậc hai vô nghiệm, liên hệ đến điều kiện f(x) > 0 hoặc f(x) < 0.
6. Tổng kết
Để $f(x) = ax^2 + bx + c ge 0$ với mọi $x in R$, điều kiện tiên quyết là $a > 0$ và $Delta le 0$. Hiểu rõ điều này, cùng với việc nắm vững định lý về dấu của tam thức bậc hai, sẽ giúp bạn giải quyết nhiều bài toán liên quan một cách hiệu quả.