Bài viết này đi sâu vào việc tính toán tích phân $int frac{dx}{5+4cos x}$ và làm thế nào các Hệ thống Đại số Máy tính (CAS) có thể mắc lỗi, mặc dù Định lý Cơ bản của Giải tích vẫn đúng. CAS có thể đưa ra kết quả khác nhau cho $int_a^b f(x) dx$ và $F(b)-F(a)$, trong đó $F$ là một nguyên hàm của $f$, ngay cả khi $f$ không có điểm kỳ dị.
Phương pháp Biến đổi Lượng giác và Giới hạn của Nó
Cách tiếp cận thủ công thường sử dụng phép thay thế $u = tan frac{x}{2}$ (xem Tangent half-angle substitution trên Wikipedia). Phép thay thế này dẫn đến:
$$int frac{dx}{5+4cos x} = int frac{1}{5+4frac{1-u^2}{1+u^2}}frac{2du}{1+u^2} = int frac{2du}{9+u^2} = frac{2}{3}arctan(frac{u}{3}) + C$$
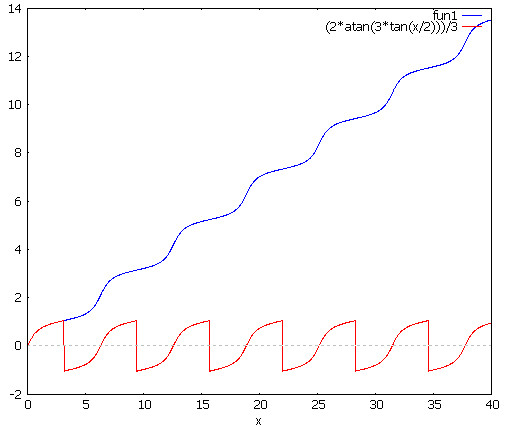
$$frac{2}{3}arctan(frac{tan frac{x}{2}}{3}) + C$$
Tuy nhiên, phép thay thế này chỉ hợp lệ trên một khoảng mà $u = tan frac{x}{2}$ là một song ánh liên tục và khả vi. Điều này không đúng trên $[0, 2pi]$ vì hàm gián đoạn tại $pi$.
Tính toán Tích phân Xác định
Để tính tích phân xác định trên $[0, 2pi]$, ta có thể chia thành hai tích phân trên $[0, pi[$ và $]pi, 2pi]$:
$$int_0^{2pi} frac{dx}{5+4cos x} = 2int_0^{pi} frac{dx}{5+4cos x} = frac{4}{3}[arctan(frac{tanfrac{x}{2}}{3})]_0^{to pi^-} = frac{2pi}{3}$$
Sai lầm của CAS và Nguyên hàm Đúng
CAS thường đưa ra một nguyên hàm chỉ hợp lệ trên một khoảng, mặc dù hàm số liên tục ở mọi nơi và do đó phải có một nguyên hàm hợp lệ trên toàn bộ $mathbb{R}$. Điều này là không chính xác.
Nguyên hàm đúng không được biểu diễn bằng một biểu thức duy nhất, mà là một tập hợp các trường hợp:
- Nếu $x in ]2kpi – pi, 2kpi + pi[$, $F(x) = frac{2}{3}arctan(frac{tanfrac{x}{2}}{3}) + frac{2}{3}kpi + C$
- Nếu $x = (2k+1)pi$, $F(x) = frac{1}{3}(2k+1)pi + C$
Trong đó $C$ là một hằng số giống nhau cho tất cả các giá trị của $x$.
Khả năng của Maple và Các Hệ thống Đại số Máy tính Khác
Với Maple, tích phân bất định cho ra kết quả đơn giản $frac{2}{3}arctan(frac{tan(frac{x}{2})}{3})$. Tuy nhiên, nó có vẻ đủ thông minh để đưa ra một lời giải đúng cho tích phân xác định, với int(1/(5-4*cos(t)), t=0..x, AllSolutions);.
Kết quả (đã dịch sang LaTeX):
$$frac{1}{3}left{ begin{array}{lr} 2pilceil -frac{pi-x}{2pi} rceil + left{ begin{array}{lr} pi, & -frac{pi-x}{2pi} in mathbb{Z} 2arctan(3tanfrac{x}{2}), & mathrm{otherwise} end{array} right., & 0 < x 0, & x = 0 end{array} right.$$
Đây không phải là đáp án đơn giản hơn $frac{x}{3} + frac{2}{3}arctan(frac{sin x}{2-cos x})$, nhưng ít nhất nó sẽ cho ra kết quả đúng cho tích phân trên $[0, 2pi]$, khi tính $F(2pi) – F(0)$, trong đó $F(x)$ là biểu thức trên.
Các hệ thống đại số máy tính khác có thể làm tương tự, có thể với các tùy chọn bổ sung (ở đây AllSolutions là cần thiết để Maple đưa ra câu trả lời đầy đủ). Điều này cho thấy sự phức tạp trong việc tính toán tích phân, đặc biệt là khi sử dụng các công cụ tự động. Hiểu rõ về các giới hạn và phương pháp của CAS là rất quan trọng để đảm bảo tính chính xác.