Trong hình học phẳng, khái niệm về đường xiên đóng vai trò quan trọng, đặc biệt khi so sánh với đường vuông góc. Để hiểu rõ hơn “đường Xiên Là Gì”, chúng ta sẽ đi sâu vào định nghĩa, các tính chất liên quan và ứng dụng của nó.
1. Định Nghĩa Đường Xiên, Đường Vuông Góc và Hình Chiếu
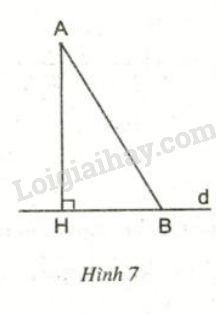
Cho một điểm (A) nằm ngoài đường thẳng (d). Từ (A), ta kẻ một đường thẳng vuông góc với (d) tại điểm (H). Lấy một điểm (B) bất kỳ trên (d) nhưng không trùng với (H). Khi đó:
- Đoạn (AH) được gọi là đoạn vuông góc, hay đường vuông góc, kẻ từ (A) đến (d). Đây là khoảng cách ngắn nhất từ điểm (A) đến đường thẳng (d).
- Đoạn (AB) được gọi là đường xiên kẻ từ (A) đến (d). Đường xiên này tạo với đường thẳng (d) một góc không vuông.
- Đoạn (HB) được gọi là hình chiếu của đường xiên (AB) lên đường thẳng (d). Độ dài hình chiếu cho biết mức độ “dài” của phần đường xiên “nằm trên” đường thẳng (d).
2. Quan Hệ Giữa Đường Vuông Góc và Đường Xiên
Trong các đường xiên và đường vuông góc kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó, đường vuông góc luôn là đường ngắn nhất. Đây là một định lý cơ bản và quan trọng. Điều này có nghĩa là, với mọi điểm (B) khác (H) trên đường thẳng (d), ta luôn có (AH < AB).
3. Quan Hệ Giữa Các Đường Xiên và Hình Chiếu Của Chúng
Khi xét nhiều đường xiên khác nhau kẻ từ một điểm đến một đường thẳng, mối quan hệ giữa độ dài đường xiên và độ dài hình chiếu của chúng trở nên thú vị.
Định lý: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó:
- Đường xiên nào có hình chiếu lớn hơn thì đường xiên đó lớn hơn. Nếu (HB > HC) thì (AB > AC).
- Đường xiên nào lớn hơn thì hình chiếu của đường xiên đó lớn hơn. Nếu (AB > AC) thì (HB > HC).
- Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau và ngược lại, nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau. Nếu (AB = AC) thì (HB = HC) và ngược lại.
4. Ứng Dụng của Đường Xiên trong Thực Tế
Hiểu rõ về đường xiên không chỉ quan trọng trong học tập mà còn có nhiều ứng dụng thực tế, ví dụ:
- Xây dựng: Tính toán độ dốc của mái nhà, đảm bảo thoát nước tốt và chịu lực hiệu quả.
- Thiết kế: Xác định góc nghiêng của các công trình kiến trúc, đảm bảo tính thẩm mỹ và ổn định.
- Thể thao: Tính toán quỹ đạo của các cú ném hoặc cú sút, tối ưu hóa hiệu suất.
- Đo đạc: Sử dụng trong các phép đo khoảng cách gián tiếp, đặc biệt ở những địa hình phức tạp.
Nắm vững khái niệm “đường xiên là gì” và các tính chất liên quan là nền tảng quan trọng để giải quyết các bài toán hình học và ứng dụng chúng vào thực tiễn.