Trong hình học phẳng, đường trung tuyến là một khái niệm quan trọng, đặc biệt khi xét đến tam giác cân. Bài viết này sẽ đi sâu vào đường Trung Tuyến Tam Giác Cân, bao gồm định nghĩa, tính chất đặc biệt, và ứng dụng của nó trong giải toán.
Định Nghĩa Đường Trung Tuyến
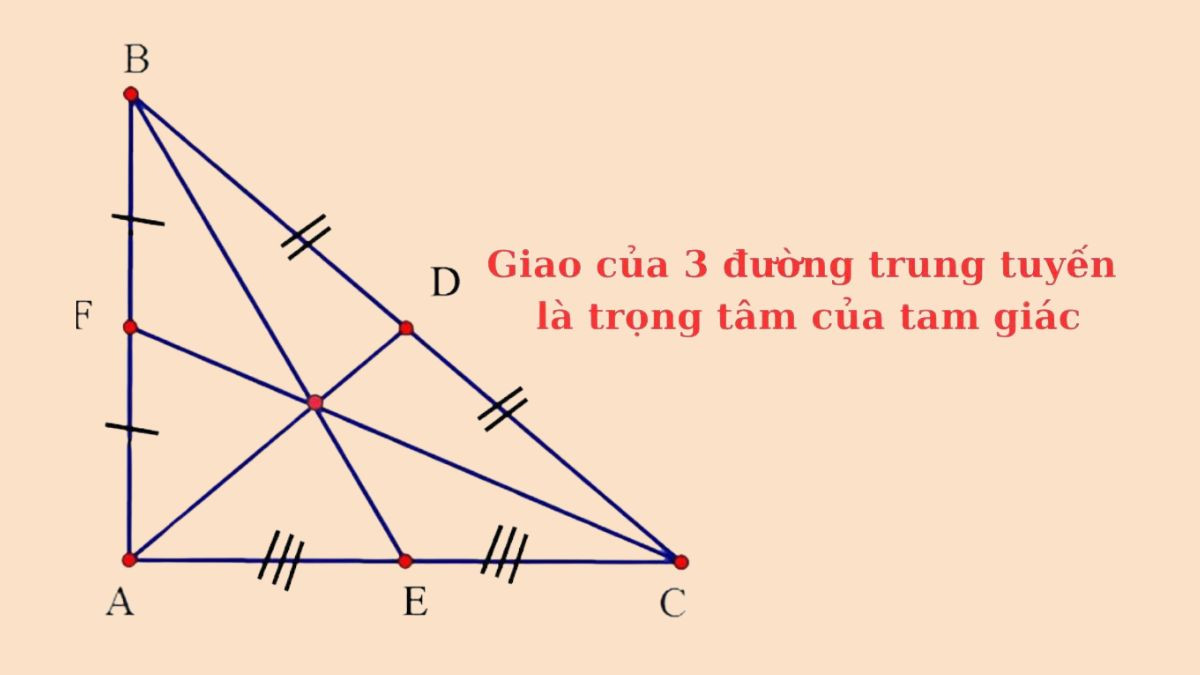
Đường trung tuyến của một tam giác là đoạn thẳng nối một đỉnh của tam giác đó với trung điểm của cạnh đối diện. Mỗi tam giác có ba đường trung tuyến, và ba đường này luôn đồng quy tại một điểm, gọi là trọng tâm của tam giác.
Đường Trung Tuyến Tam Giác Cân: Tính Chất Đặc Biệt
Tam giác cân là tam giác có ít nhất hai cạnh bằng nhau. Trong tam giác cân, đường trung tuyến xuất phát từ đỉnh góc cân có những tính chất đặc biệt quan trọng:
- Vừa là đường trung tuyến, vừa là đường cao: Đường trung tuyến kẻ từ đỉnh góc cân đến cạnh đáy đồng thời là đường cao, tức là nó vuông góc với cạnh đáy.
- Vừa là đường trung tuyến, vừa là đường phân giác: Đường trung tuyến này cũng là đường phân giác của góc ở đỉnh, chia góc đó thành hai góc bằng nhau.
Tính chất này giúp đơn giản hóa nhiều bài toán liên quan đến tam giác cân, đặc biệt là trong các bài toán chứng minh và tính toán.
Các Tính Chất Chung của Đường Trung Tuyến
Ngoài những tính chất đặc biệt trong tam giác cân, đường trung tuyến còn có những tính chất chung áp dụng cho mọi tam giác:
- Giao điểm của ba đường trung tuyến là trọng tâm: Trọng tâm chia mỗi đường trung tuyến thành hai đoạn, đoạn nối từ đỉnh đến trọng tâm dài gấp đôi đoạn nối từ trọng tâm đến trung điểm cạnh đối diện.
- Đường trung tuyến chia tam giác thành hai tam giác có diện tích bằng nhau.
Định Lý Liên Quan Đến Đường Trung Tuyến
Có một số định lý quan trọng liên quan đến đường trung tuyến, giúp chúng ta giải quyết các bài toán phức tạp hơn:
- Định lý về trọng tâm: Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó.
- Định lý Apollonius: Cho tam giác ABC, gọi M là trung điểm của BC. Khi đó, AB² + AC² = 2(AM² + BM²).
Công Thức Tính Độ Dài Đường Trung Tuyến
Độ dài đường trung tuyến có thể được tính bằng công thức sau:
Cho tam giác ABC với các cạnh a, b, c và đường trung tuyến $m_a$ kẻ từ đỉnh A đến trung điểm cạnh a, ta có:
$m_a = frac{1}{2}sqrt{2b^2 + 2c^2 – a^2}$
Tương tự, ta có thể tính $m_b$ và $m_c$. Công thức này rất hữu ích khi biết độ dài ba cạnh của tam giác và cần tìm độ dài đường trung tuyến.
Ứng Dụng của Đường Trung Tuyến Tam Giác Cân
Đường trung tuyến tam giác cân có nhiều ứng dụng trong giải toán hình học, bao gồm:
- Chứng minh các tính chất hình học: Sử dụng tính chất đường trung tuyến vừa là đường cao, vừa là đường phân giác để chứng minh các tam giác bằng nhau, đồng dạng.
- Tính diện tích và các yếu tố khác của tam giác: Dựa vào đường trung tuyến, ta có thể chia tam giác thành các phần nhỏ hơn, dễ tính toán hơn.
- Giải các bài toán thực tế: Áp dụng vào các bài toán đo đạc, thiết kế, xây dựng, nơi mà tính đối xứng và cân bằng là yếu tố quan trọng.
Bài Tập Vận Dụng
Bài tập 1: Cho tam giác ABC cân tại A, biết AB = AC = 10cm, BC = 12cm. Tính độ dài đường trung tuyến AM.
Giải:
Vì tam giác ABC cân tại A, nên đường trung tuyến AM cũng là đường cao. Suy ra, tam giác AMB vuông tại M.
Ta có BM = MC = BC/2 = 6cm.
Áp dụng định lý Pythagoras vào tam giác AMB:
$AM = sqrt{AB^2 – BM^2} = sqrt{10^2 – 6^2} = sqrt{64} = 8cm$
Vậy độ dài đường trung tuyến AM là 8cm.
Bài tập 2: Cho tam giác ABC có AB = 6, BC = 8, CA = 10. Chứng minh rằng tam giác ABC là tam giác vuông và tính độ dài đường trung tuyến ứng với cạnh huyền.
Giải:
Ta thấy $AB^2 + BC^2 = 6^2 + 8^2 = 36 + 64 = 100 = CA^2$. Theo định lý Pythagoras đảo, tam giác ABC vuông tại B.
Đường trung tuyến ứng với cạnh huyền AC bằng một nửa cạnh huyền. Vậy, $m_b = frac{AC}{2} = frac{10}{2} = 5$.
Kết Luận
Đường trung tuyến tam giác cân là một khái niệm quan trọng trong hình học, với nhiều tính chất và ứng dụng hữu ích. Việc nắm vững kiến thức về đường trung tuyến, đặc biệt trong tam giác cân, giúp chúng ta giải quyết các bài toán hình học một cách hiệu quả hơn. Hy vọng bài viết này đã cung cấp cho bạn những thông tin cần thiết và hữu ích về đường trung tuyến tam giác cân.