1. Tính chất cơ bản của đường phân giác
Đường phân giác của một góc là tia nằm giữa hai cạnh của góc đó và chia góc đó thành hai góc bằng nhau. Điểm nằm trên đường phân giác của một góc thì cách đều hai cạnh của góc đó. Ngược lại, điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên đường phân giác của góc đó. Tập hợp các điểm nằm bên trong một góc và cách đều hai cạnh của góc là đường phân giác của góc đó.
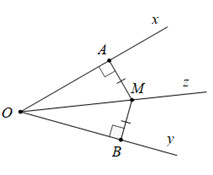Minh họa tia phân giác Oz của góc xOy
Hình ảnh minh họa tia Oz là đường phân giác của góc xOy. Điểm M nằm trên Oz và cách đều hai cạnh Ox và Oy, thể hiện tính chất cơ bản của đường phân giác.
2. Đường phân giác trong tam giác cân
Trong tam giác cân, đường phân giác có những tính chất đặc biệt quan trọng, giúp giải quyết nhiều bài toán hình học.
Định lý: Trong một tam giác cân, đường phân giác của góc ở đỉnh đồng thời là đường trung tuyến, đường cao và đường trung trực của tam giác đó. Điều này có nghĩa là nó chia cạnh đáy thành hai đoạn bằng nhau và vuông góc với cạnh đáy.
Hình ảnh minh họa tam giác ABC cân tại A với AD là đường trung tuyến. Vì tam giác cân, AD cũng là đường phân giác của góc A, thể hiện mối liên hệ giữa đường trung tuyến và đường phân giác trong tam giác cân.
Ví dụ: Cho tam giác ABC cân tại A, AD là đường phân giác của góc A. Khi đó, AD cũng là đường trung tuyến, suy ra BD = DC. Đồng thời, AD vuông góc với BC.
3. Ứng dụng của đường Phân Giác Trong Tam Giác Cân
- Chứng minh các đoạn thẳng bằng nhau: Sử dụng tính chất đường phân giác vừa là đường trung tuyến để chứng minh các đoạn thẳng liên quan bằng nhau.
- Chứng minh các góc bằng nhau: Vì đường phân giác chia góc ở đỉnh thành hai góc bằng nhau, ta có thể sử dụng để chứng minh các góc khác bằng nhau thông qua các tính chất của tam giác cân.
- Tính toán độ dài: Nếu biết độ dài một số cạnh và góc của tam giác cân, ta có thể sử dụng các tính chất của đường phân giác để tính toán độ dài các cạnh và góc còn lại.
- Giải các bài toán liên quan đến tính đối xứng: Tam giác cân có tính đối xứng qua đường phân giác của góc ở đỉnh, do đó đường phân giác đóng vai trò quan trọng trong các bài toán liên quan đến tính đối xứng.
4. Ba đường phân giác của tam giác
Ba đường phân giác của một tam giác bất kỳ đồng quy tại một điểm. Điểm này gọi là tâm đường tròn nội tiếp của tam giác, và nó cách đều ba cạnh của tam giác đó.
Hình ảnh minh họa tam giác ABC với ba đường phân giác cắt nhau tại điểm I. Điểm I là tâm đường tròn nội tiếp tam giác ABC và cách đều ba cạnh của tam giác.
5. Các dạng bài toán thường gặp
- Chứng minh hai đoạn thẳng bằng nhau, hai góc bằng nhau: Sử dụng tính chất của đường phân giác và các tính chất của tam giác cân để chứng minh.
- Chứng minh một đường thẳng là tia phân giác của một góc: Sử dụng định nghĩa hoặc tính chất của đường phân giác.
- Bài toán về đường phân giác với các tam giác đặc biệt (tam giác cân, tam giác đều): Áp dụng các định lý và tính chất riêng của tam giác cân và tam giác đều để giải quyết.